- Introduction
L’algorithme des k plus proches voisins appartient à la famille des algorithmes d’apprentissage automatique (machine learning).
L’idée d’apprentissage automatique ne date pas d’hier, puisque le terme de machine learning a été utilisé pour la première fois par
l’informaticien américain Arthur Samuel en 1959. Les algorithmes d’apprentissage automatique ont connu un fort regain d’intérêt
au début des années 2000 notamment grâce à la quantité de données disponibles sur internet.
L’algorithme des k plus proches voisins est un algorithme d’apprentissage supervisé, il est nécessaire d’avoir des données labellisées. À partir d’un ensemble E de données labellisées, il sera possible de classer (déterminer le label) d’une nouvelle donnée (donnée n’appartenant pas à E). À noter qu’il est aussi possible d’utiliser l’algorithme des k plus proches voisins à des fins de régression (on cherche à déterminer une valeur à la place d’une classe), mais cet aspect des choses ne sera pas abordé ici. L’algorithme des k plus proches voisins est une bonne introduction aux principes des algorithmes d’apprentissage automatique, il est en effet relativement simple à appréhender (l’explication donnée aux élèves peut être très visuelle). Cette première approche des algorithmes d’apprentissage peut aussi amener les élèves à réfléchir sur l’utilisation de leurs données personnelles (même si ce sujet a déjà abordé auparavant) : de nombreuses sociétés (exemple les GAFAM) utilisent les données concernant leurs utilisateurs afin de ”nourrir” des algorithmes de machine learning qui permettront à ces sociétés d’en savoir toujours plus sur nous et ainsi de mieux cerné nos ”besoins” en termes de consommation.
- Principe de l’algorithme
L’algorithme de k plus proches voisins ne nécessite pas de phase d’apprentissage à proprement parler, il faut juste stocker le jeu de
données d’apprentissage.
Soit un ensemble E contenant n données labellisées : E = {(yi
, x⃗i)} avec i compris entre 1 et n, où yi correspond à la classe
(le label) de la donnée i et où le vecteur x⃗i de dimension p (x⃗i = (x1i
, x2i, …, xpi)) représente les variables prédictrices de la donnée i. Soit une donnée u qui n’appartient pas à E et qui ne possède pas de label (u est uniquement caractérisée par un vecteur x⃗u de dimension p). Soit d une fonction qui renvoie la distance entre la donnée u et une donnée quelconque appartenant à E. Soit un entier k inférieur ou égal à n. Voici le principe de l’algorithme de k plus proches voisins :
▷ On calcule les distances entre la donnée u et chaque donnée appartenant à E à l’aide de la fonction d
▷ On retient les k données du jeu de données E les plus proches de u
▷ On attribue à u la classe qui est la plus fréquente parmi les k données les plus proches.
- Étude d’un exemple
3.1. Les données
Nous avons choisi ici de nous baser sur le jeu de données ”iris de Fisher” (il existe de nombreuses autres possibilités). Ce jeu de
données est composé de 50 entrées, pour chaque entrée nous avons :
▷ la longueur des sépales (en cm)
▷ la largeur des sépales (en cm)
▷ la longueur des pétales (en cm)
▷ la largeur des pétales (en cm)
▷ l’espèce d’iris : Iris setosa, Iris virginica ou Iris versicolor (label)
Il est possible de télécharger ces données au format csv, par exemple sur le site GitHub Gist ou en le téléchargeant ici
Une fois ces données téléchargées, Il est nécessaire de les modifier à l’aide d’un tableur :
▷ dans un souci de simplification, nous avons choisi de travailler uniquement sur la taille des pétales, nous allons donc supprimer les colonnes ”sepal_length” et ”sepal_width”
▷ il est nécessaire d’encoder les espèces avec des chiffres : 0 pour Iris setosa, 1 pour Iris virginica et 2 pour Iris versicolor (ce
processus d’encodage des données textuelles est relativement classique en apprentissage automatique).
3.2. Bibliothèques Python utilisées
Nous allons utiliser 3 bibliothèques Python :
▷ Pandas [3] qui va nous permettre d’importer les données issues du fichier csv
▷ Matplotlib [4] qui va nous permettre de visualiser les données (tracer des graphiques)
▷ Scikit-learn [5] qui propose une implémentation de l’algorithme des k plus proches voisins.
Ces bibliothèques sont facilement installables notamment en utilisant la distribution Anaconda (ou Miniconda).
3.3. Première visualisation des données
Une fois le fichier csv modifié, il est possible d’écrire un programme permettant de visualiser les données sous forme de graphique
(abscisse : ”petal_length”, ordonnée : ”petal_width”) :
import pandas
import matplotlib.pyplot as plt
iris=pandas.read_csv("iris.csv")
x=iris.loc[:,"petal_length"]
y=iris.loc[:,"petal_width"]
lab=iris.loc[:,"species"]
plt.scatter(x[lab == 0], y[lab == 0], color='g', label='setosa')
plt.scatter(x[lab == 1], y[lab == 1], color='r', label='virginica')
plt.scatter(x[lab == 2], y[lab == 2], color='b', label='versicolor')
plt.scatter(2.5, 0.75, color='k')
plt.legend()
plt.show()
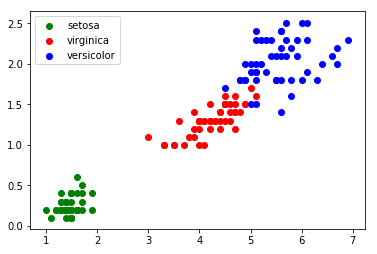
3.4. Utilisation de l’algorithme des k plus proches voisins Le graphique ci-dessus (figure 1) montre que les 3 classes (Iris setosa, Iris virginica et Iris versicolor) sont relativement bien séparées. On peut alors ajouter une donnée non labellisée n’appartenant pas à l’ensemble d’origine (voir figure 2) :
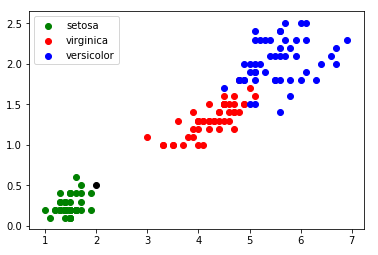
Dans l’exemple ci-dessus (figure 2) les élèves n’auront aucune difficulté à déterminer l’espèce de l’iris qui a été ajouté au jeu de données.
Dans certains cas (exemple : largeur pétale = 0,75 cm ; longueur pétale = 2,5 cm) il est un peu plus difficile de se prononcer ”au premier coup d’oeil” (voir figure 3) :
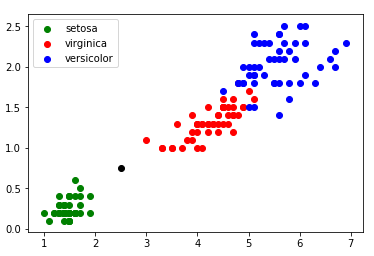
À partir de l’exemple ci-dessus (voir figure 3), il est possible de demander aux élèves de proposer une méthode permettant de traiter
ce genre de cas litigieux. L’enseignant peut, grâce à une série de ”questions-réponses”, amener doucement les élèves à la solution
proposée par l’algorithme des k plus proches voisins :
▷ on calcule la distance entre notre point (largeur du pétale = 0,75 cm ; longueur du pétale = 2,5 cm) et chaque point issu du
jeu de données ”iris” (à chaque fois c’est un calcul de distance entre 2 points tout ce qu’il y a de plus classique) ;
▷ on sélectionne uniquement les k distances les plus petites (les k plus proches voisins) ;
▷ parmi les k plus proches voisins, on détermine quelle est l’espèce majoritaire. On associe à notre ”iris mystère” cette ”espèce
majoritaire parmi les k plus proches voisins”.
Dans l’exemple évoqué ci-dessus (largeur pétale = 0,75 cm ; longueur pétale = 2,5 cm), pour k=3, nous obtenons graphiquement :
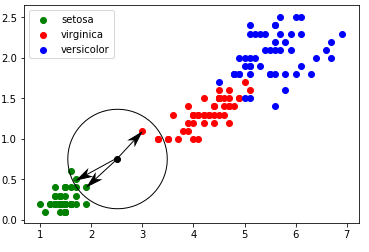
Un iris ayant une largeur de pétale égale à 0,75 cm et une longueur de pétale égale à 2,5 cm a une ”forte” probabilité (cette notion
de probabilité d’obtenir un résultat correct grâce à cet algorithme, bien que très intéressante, pourra difficilement être abordée avec
des élèves de première) d’appartenir à l’espèce setosa.
3.5. Utilisation de scikit-learn (à installer si absente de votre éditeur)
La bibliothèque Python scikit-learn propose un grand nombre d’algorithmes lié à l’apprentissage automatique (c’est sans aucun
doute la bibliothèque la plus utilisée en apprentissage automatique). Parmi tous ces algorithmes, scikit-learn propose l’algorithme
des k plus proches voisins. Voici un programme Python permettant de résoudre le problème évoqué ci-dessus (largeur pétale = 0,75
cm ; longueur pétale = 2,5 cm) :
import pandas
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
#traitement CSV
iris=pandas.read_csv("iris.csv")
x=iris.loc[:,"petal_length"]
y=iris.loc[:,"petal_width"]
lab=iris.loc[:,"species"]
#fin traitement CSV
#valeurs
longueur=2.5
largeur=0.75
k=3
#fin valeurs
#graphique
plt.scatter(x[lab == 0], y[lab == 0], color='g', label='setosa')
plt.scatter(x[lab == 1], y[lab == 1], color='r', label='virginica')
plt.scatter(x[lab == 2], y[lab == 2], color='b', label='versicolor')
plt.scatter(longueur, largeur, color='k')
plt.legend()
#fin graphique
#algo knn
d=list(zip(x,y))
model = KNeighborsClassifier(n_neighbors=k)
model.fit(d,lab)
prediction= model.predict([[longueur,largeur]])
#fin algo knn
#Affichage résultats
txt="Résultat : "
if prediction[0]==0:
txt=txt+"setosa"
if prediction[0]==1:
txt=txt+"virginica"
if prediction[0]==2:
txt=txt+"versicolor"
plt.text(3,0.5, f"largeur : {largeur} cm longueur : {longueur} cm", fontsize=12)
plt.text(3,0.3, f"k : {k}", fontsize=12)
plt.text(3,0.1, txt, fontsize=12)
#fin affichage résultats
plt.show()
Nous obtenons le résultat suivant (voir figure 5) :
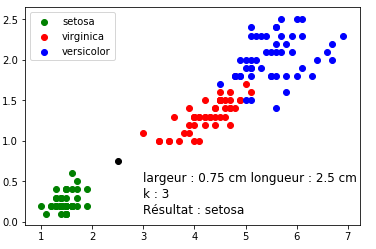
Il est ensuite possible de demander aux élèves de m le programme ci-dessus afin d’étudier les changements induits par la
modification du paramètre k (notamment pour k=5) en gardant toujours les mêmes valeurs de largeur et de longueur (largeur pétale
= 0,75 cm ; longueur pétale = 2,5 cm).
Pour terminer, il est aussi possible de demander aux élèves de travailler avec d’autres valeurs de longueur et largeur.
- Possibilité de projet
Il est possible, dans le cadre d’un projet, de faire travailler les élèves sur un autre jeu de données, par exemple, ”Prédire les survivants
du Titanic”. Le jeu de données peut être récupéré sur le site kaggle [6]. Le label est ”survivant” ou ”décédé”. Il sera nécessaire de
retravailler les données comme nous l’avons fait pour le jeu de données ”Iris” (supprimer des colonnes, encodage…). Dans ce projet
il sera possible de faire travailler les élèves sur des vecteurs d’entrée de dimension supérieure à 2 (le genre, l’âge, la classe occupée
par le passager sur le bateau, …).
voici un lien vers le projet Titanic développé par Benoit Fourlegnie:



 .
.