Algorithmes gloutons

14 septembre 2020 icnisnboissy

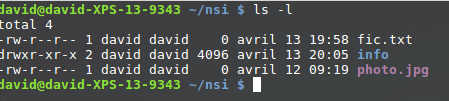
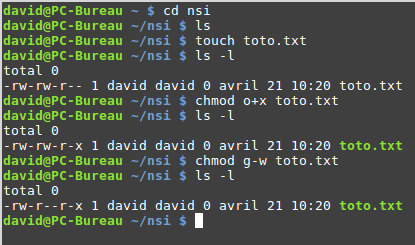
Présentation des d’algorithmes gloutons avec exemples et TD. cet article est une copie d’un article du site www.math93.com/ , vous pouvez le voir ici .

Voici une petite vidéo sur les algorithmes Glouton

Présentation de la notion d’algorithme glouton.
1. Les problèmes d’optimisation.
2. Résoudre un problème d’optimisation : les algorithmes gloutons
Le problème du rendu de monnaie.
Le TD sur les algorithmes gloutons et le rendu de monnaie.

1. Présentation de la notion d’algorithme glouton

1.1. Les problèmes d’optimisation

L’optimisation est une branche des mathématiques cherchant à modéliser, à analyser et à résoudre les problèmes qui consistent à minimiser ou maximiser une fonction sur un ensemble.

Les problèmes d’optimisation classiques sont par exemple :

la répartition optimale de tâches suivant des critères précis (emploi du temps avec plusieurs contraintes) ;

le problème du rendu de monnaie ;

la recherche d’un plus court chemin dans un graphe ;

le problème du voyageur de commerce.

1.2. Résoudre un problème d’optimisation : les algorithmes gloutons

De nombreuses techniques informatiques sont susceptibles d’apporter une solution exacte ou approchée à ces problèmes.

Recherche de toutes les solutions
La technique la plus basique pour résoudre ce type de problème d’optimisation consiste à énumérer de façon exhaustive toutes les solutions possibles, puis à choisir la meilleure. Cette approche par force brute, impose souvent un coût en temps trop important pour être utilisée.
Les algorithmes gloutons
Un algorithme glouton (greedy algorithm) est un algorithme qui suit le principe de faire, étape par étape, un choix optimum local.
Au cours de la construction de la solution, l’algorithme résout une partie du problème puis se focalise ensuite sur le sous-problème restant à résoudre.
La méthode gloutonne consiste à choisir des solutions locales optimales d’un problème dans le but d’obtenir une solution optimale globale au problème.
- Le principal avantage des algorithmes gloutons est leur facilité de mise en œuvre.
- Le principal défaut est qu’il ne renvoie pas toujours la solution optimale nous le verrons.
- Dans certaines situations dites canoniques, il arrive qu’ils renvoient non pas un optimum mais l’optimum d’un problème

2. Le problème du rendu de monnaie

Un achat dit en espèces se traduit par un échange de pièces et de billets. Dans la suite, les pièces désignent indifféremment les véritables pièces que les billets.

Supposons qu’un achat induise un rendu de 49 euros on considérant pour simplifier que les ‘pièces’ prennent les valeurs 1, 2, 5, 10, 20, 50, 100 euros. Quelles pièces peuvent être rendues ?

49=4×10+1×5+2×2

soit 7 pièces au total
(Quatre pièces de 10 euros, 1 pièce de 5 euros et deux pièces de 2 euros.) ou 49=9×5+2×2 soit 11 pièces au total ou 49=9×5+4×1 soit 13 pièces au total ou 49=49×1

soit 49 pièces au total

Le problème du rendu de monnaie consiste à déterminer la solution avec le nombre minimal de pièces.

Rendre 49 euros avec un minimum de pièces est un problème d’optimisation. En pratique, tout individu met en œuvre un algorithme glouton.

Il choisit d’abord la plus grandeur valeur de monnaie, parmi 1, 2, 5, 10, contenue dans 49 euros.
En l’occurrence, quatre fois une pièce de 10 euros.
La somme de 9 euros restant à rendre, il choisit une pièce de 5 euros,
Puis deux pièces de 2 euros.

Solution optimale et système canonique du rendu de monnaie

Cette stratégie gagnante pour la somme de 49 euros l’est-elle pour n’importe quelle somme à rendre ?

Un système canonique
- On peut montrer que l’algorithme glouton du rendu de monnaie renvoie une solution optimale pour le système monétaire français
  {1,2,5,10,20,50,100}
- Pour cette raison, un tel système de monnaie est qualiﬁé de canonique.

Des systèmes non canoniques

D ’autres systèmes ne sont pas canoniques. L’algorithme glouton ne répond alors pas de manière optimale.
Par exemple, avec le système {1,3,6,12,24,30},l’algorithme glouton répond en proposant le rendu : 49=30+12+6+1 soit 4 pièces alors que la solution optimale est 49=2×24+1

soit 3 pièces.

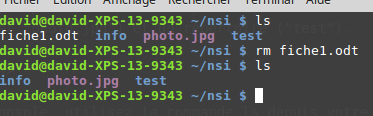
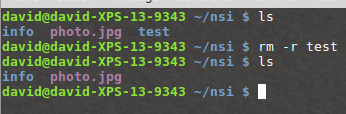
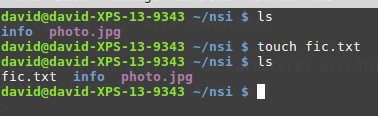
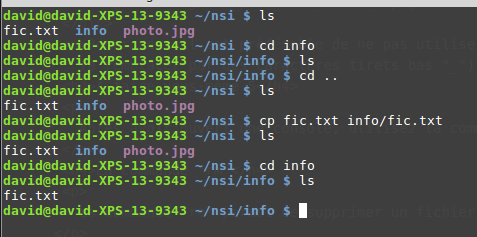
3. Le TD sur les algorithmes gloutons et le rendu de monnaie

Prérequis au TD
- Python : liste, parcours de listes.

On cherche à implémenter un algorithme glouton de rendu de monnaie en ne considérant que des valeurs entières des pièces du système.
Par ailleurs, la plus petite pièce du système sera toujours 1, on est ainsi certain de pouvoir rendre la monnaie quelque soit la somme choisie.

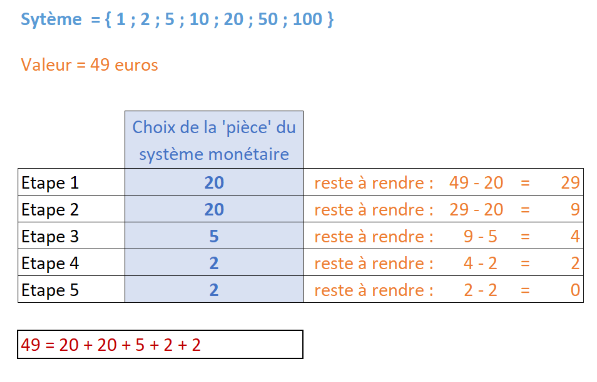
Fonctionnement de l’algorithme glouton du rendu de monnaie

On choisit un système de monnaies, par exemple systeme=[1,2,5,10,20,50,100]
On choisit une valeur, par exemple valeur=49 euros .
On choisit la plus grande ‘pièce’ du système inférieure à la valeur et on l’ajoute à la liste des pièces à rendre.
On calcule le reste à rendre et on recommence jusqu’à obtenir un reste à rendre nul.

Exercice 1

Écrire une une fonction python qui reçoit deux arguments – la somme à rendre et le système de monnaie – et qui renvoie la liste des pièces choisies par l’algorithme glouton.
Tester votre fonction avec les valeurs et les systèmes proposés dans les exemples du cours ci-dessus.
Inventez un système non canonique différent de celui de l’exemple (mais toujours de valeur minimale 1) et trouver un exemple qui le prouve.
Votre fonction devra donc donner une solution mais qui n’est pas optimale.
Complément : créer un programme (ou une autre fonction) qui va afficher toutes les informations suivantes :
49=4×10+1×5+2×2
Soit 7 pièces au total
C’est à dire : Quatre pièces de 10 euros, 1 pièce de 5 euros et deux pièces de 2 euros.

Aide pour l’exercice 1:

Etape 1
- Définissons le système de pièces à l’aide d’un tableau nommé systeme constitué des valeurs des pièces classées par valeurs croissantes (de plus petite pièce 1).
- On définit aussi une valeur à tester, les 49 euros de l’exemple ci-dessus, dans la variable valeur.
- Ainsi que l’indice i de la plus grande des pièces de systeme.

# valeurs des pièces du système choisi
systeme = [1,2,5,10,20,50,100]
# valeur à tester (par exemple 49 euros)
valeur=49
# indice de la première pièce à comparer à la somme à rendre
i = len(systeme) - 1

Etape 2 : Fonctionnement de l’algorithme
- On cherche à déterminer les pièces à rendre pour la variable valeur.
- Initialisations
  - La somme à rendre à rendre est initialement stockée dans la variable somme_a_rendre. On l’initialise donc à valeur.
  - liste_pieces, la liste des pièces à rendre est initialisée à une liste vide
  - i = len(systeme) - 1 : indice de la première pièce à comparer à la somme à rendre
- On boucle tant que somme_a_rendre > 0
  - La variable piece prend la valeur de la pièce de systeme d’indice i
  - Si somme_a_rendre < piece
    - Alors i pend la valeur i-1
  - Sinon
    - alors on ajoute la piece à la liste des pièces à rendre liste_pieces
    - on enlève la valeur de piece de somme_a_rendre
- On renvoie la liste : liste_pieces

Exercice 2

On cherche maintenant à généraliser notre algorithme avec le système de pièces et de billets utilisées en Europe et des valeurs décimales.
On va donc considérer un système composé de pièces et de billets :
- Les pièces (en euros) : 0,01 – 0,02 – 0,05 – 0,10 – 0,20 – 0,50 – 1 – 2 ;
- Les billets (en euros) : 5 – 10 – 20 – 50 – 100 – 200 – 500.

Modifier donc votre programme afin qu’il affiche le nombre les pièces à rendre et les billets.
Tester les avec plusieurs exemples.
Et si il n’y avait ni billet de 5, ni billet de 10 euros.
Montrer avec un exemple bien choisi que la solution donnée par l’algorithme n’est pas optimale

Exercice 3 – Une pièce de 7 euros

On peut se demander pourquoi il n’y a pas de pièce de 7 euros par exemple.
En fait c’est parce que si tel était le cas, l’algorithme glouton de rendu de monnaie ne serait plus optimal.

Tester votre algorithme en ajoutant une pièce de 7 euros dans le système.
Trouver un exemple qui renvoie une solution qui n’est pas optimale.

NSI, Algorithmique

Algorithme des k plus proches voisins

14 septembre 2020 thierryp

Introduction
L’algorithme des k plus proches voisins appartient à la famille des algorithmes d’apprentissage automatique (machine learning).
L’idée d’apprentissage automatique ne date pas d’hier, puisque le terme de machine learning a été utilisé pour la première fois par
l’informaticien américain Arthur Samuel en 1959. Les algorithmes d’apprentissage automatique ont connu un fort regain d’intérêt
au début des années 2000 notamment grâce à la quantité de données disponibles sur internet.
L’algorithme des k plus proches voisins est un algorithme d’apprentissage supervisé, il est nécessaire d’avoir des données labellisées. À partir d’un ensemble E de données labellisées, il sera possible de classer (déterminer le label) d’une nouvelle donnée (donnée n’appartenant pas à E). À noter qu’il est aussi possible d’utiliser l’algorithme des k plus proches voisins à des fins de régression (on cherche à déterminer une valeur à la place d’une classe), mais cet aspect des choses ne sera pas abordé ici. L’algorithme des k plus proches voisins est une bonne introduction aux principes des algorithmes d’apprentissage automatique, il est en effet relativement simple à appréhender (l’explication donnée aux élèves peut être très visuelle). Cette première approche des algorithmes d’apprentissage peut aussi amener les élèves à réfléchir sur l’utilisation de leurs données personnelles (même si ce sujet a déjà abordé auparavant) : de nombreuses sociétés (exemple les GAFAM) utilisent les données concernant leurs utilisateurs afin de ”nourrir” des algorithmes de machine learning qui permettront à ces sociétés d’en savoir toujours plus sur nous et ainsi de mieux cerné nos ”besoins” en termes de consommation.

Principe de l’algorithme
L’algorithme de k plus proches voisins ne nécessite pas de phase d’apprentissage à proprement parler, il faut juste stocker le jeu de
données d’apprentissage.
Soit un ensemble E contenant n données labellisées : E = {(yi
, x⃗i)} avec i compris entre 1 et n, où yi correspond à la classe
(le label) de la donnée i et où le vecteur x⃗i de dimension p (x⃗i = (x1i
, x2i, …, xpi)) représente les variables prédictrices de la donnée i. Soit une donnée u qui n’appartient pas à E et qui ne possède pas de label (u est uniquement caractérisée par un vecteur x⃗u de dimension p). Soit d une fonction qui renvoie la distance entre la donnée u et une donnée quelconque appartenant à E. Soit un entier k inférieur ou égal à n. Voici le principe de l’algorithme de k plus proches voisins :
▷ On calcule les distances entre la donnée u et chaque donnée appartenant à E à l’aide de la fonction d
▷ On retient les k données du jeu de données E les plus proches de u
▷ On attribue à u la classe qui est la plus fréquente parmi les k données les plus proches.

Étude d’un exemple
3.1. Les données
Nous avons choisi ici de nous baser sur le jeu de données ”iris de Fisher” (il existe de nombreuses autres possibilités). Ce jeu de
données est composé de 50 entrées, pour chaque entrée nous avons :
▷ la longueur des sépales (en cm)
▷ la largeur des sépales (en cm)
▷ la longueur des pétales (en cm)
▷ la largeur des pétales (en cm)
▷ l’espèce d’iris : Iris setosa, Iris virginica ou Iris versicolor (label)
Il est possible de télécharger ces données au format csv, par exemple sur le site GitHub Gist ou en le téléchargeant ici
Une fois ces données téléchargées, Il est nécessaire de les modifier à l’aide d’un tableur :
▷ dans un souci de simplification, nous avons choisi de travailler uniquement sur la taille des pétales, nous allons donc supprimer les colonnes ”sepal_length” et ”sepal_width”
▷ il est nécessaire d’encoder les espèces avec des chiffres : 0 pour Iris setosa, 1 pour Iris virginica et 2 pour Iris versicolor (ce
processus d’encodage des données textuelles est relativement classique en apprentissage automatique).
3.2. Bibliothèques Python utilisées
Nous allons utiliser 3 bibliothèques Python :
▷ Pandas [3] qui va nous permettre d’importer les données issues du fichier csv
▷ Matplotlib [4] qui va nous permettre de visualiser les données (tracer des graphiques)
▷ Scikit-learn [5] qui propose une implémentation de l’algorithme des k plus proches voisins.
Ces bibliothèques sont facilement installables notamment en utilisant la distribution Anaconda (ou Miniconda).
3.3. Première visualisation des données
Une fois le fichier csv modifié, il est possible d’écrire un programme permettant de visualiser les données sous forme de graphique
(abscisse : ”petal_length”, ordonnée : ”petal_width”) :

iris Télécharger

import pandas
import matplotlib.pyplot as plt
iris=pandas.read_csv("iris.csv")
x=iris.loc[:,"petal_length"]
y=iris.loc[:,"petal_width"]
lab=iris.loc[:,"species"]
plt.scatter(x[lab == 0], y[lab == 0], color='g', label='setosa')
plt.scatter(x[lab == 1], y[lab == 1], color='r', label='virginica')
plt.scatter(x[lab == 2], y[lab == 2], color='b', label='versicolor')
plt.scatter(2.5, 0.75, color='k')
plt.legend()
plt.show()

FIGURE 1 – Représentation graphique des données

3.4. Utilisation de l’algorithme des k plus proches voisins Le graphique ci-dessus (figure 1) montre que les 3 classes (Iris setosa, Iris virginica et Iris versicolor) sont relativement bien séparées. On peut alors ajouter une donnée non labellisée n’appartenant pas à l’ensemble d’origine (voir figure 2) :

FIGURE 2 – Ajout d’une donnée non labellisée

Dans l’exemple ci-dessus (figure 2) les élèves n’auront aucune difficulté à déterminer l’espèce de l’iris qui a été ajouté au jeu de données.
Dans certains cas (exemple : largeur pétale = 0,75 cm ; longueur pétale = 2,5 cm) il est un peu plus difficile de se prononcer ”au premier coup d’oeil” (voir figure 3) :

À partir de l’exemple ci-dessus (voir figure 3), il est possible de demander aux élèves de proposer une méthode permettant de traiter
ce genre de cas litigieux. L’enseignant peut, grâce à une série de ”questions-réponses”, amener doucement les élèves à la solution
proposée par l’algorithme des k plus proches voisins :
▷ on calcule la distance entre notre point (largeur du pétale = 0,75 cm ; longueur du pétale = 2,5 cm) et chaque point issu du
jeu de données ”iris” (à chaque fois c’est un calcul de distance entre 2 points tout ce qu’il y a de plus classique) ;
▷ on sélectionne uniquement les k distances les plus petites (les k plus proches voisins) ;

▷ parmi les k plus proches voisins, on détermine quelle est l’espèce majoritaire. On associe à notre ”iris mystère” cette ”espèce
majoritaire parmi les k plus proches voisins”.
Dans l’exemple évoqué ci-dessus (largeur pétale = 0,75 cm ; longueur pétale = 2,5 cm), pour k=3, nous obtenons graphiquement :

FIGURE 4 – 3 plus proches voisins dans le cas : largeur pétale = 0,75 cm ; longueur pétale = 2,5 cm

Un iris ayant une largeur de pétale égale à 0,75 cm et une longueur de pétale égale à 2,5 cm a une ”forte” probabilité (cette notion
de probabilité d’obtenir un résultat correct grâce à cet algorithme, bien que très intéressante, pourra difficilement être abordée avec
des élèves de première) d’appartenir à l’espèce setosa.

3.5. Utilisation de scikit-learn (à installer si absente de votre éditeur)
La bibliothèque Python scikit-learn propose un grand nombre d’algorithmes lié à l’apprentissage automatique (c’est sans aucun
doute la bibliothèque la plus utilisée en apprentissage automatique). Parmi tous ces algorithmes, scikit-learn propose l’algorithme
des k plus proches voisins. Voici un programme Python permettant de résoudre le problème évoqué ci-dessus (largeur pétale = 0,75
cm ; longueur pétale = 2,5 cm) :

import pandas
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier

#traitement CSV
iris=pandas.read_csv("iris.csv")
x=iris.loc[:,"petal_length"]
y=iris.loc[:,"petal_width"]
lab=iris.loc[:,"species"]
#fin traitement CSV

#valeurs
longueur=2.5
largeur=0.75
k=3
#fin valeurs

#graphique
plt.scatter(x[lab == 0], y[lab == 0], color='g', label='setosa')
plt.scatter(x[lab == 1], y[lab == 1], color='r', label='virginica')
plt.scatter(x[lab == 2], y[lab == 2], color='b', label='versicolor')
plt.scatter(longueur, largeur, color='k')
plt.legend()
#fin graphique

#algo knn
d=list(zip(x,y))
model = KNeighborsClassifier(n_neighbors=k)
model.fit(d,lab)
prediction= model.predict([[longueur,largeur]])
#fin algo knn

#Affichage résultats
txt="Résultat : "
if prediction[0]==0:
    txt=txt+"setosa"
if prediction[0]==1:
    txt=txt+"virginica"
if prediction[0]==2:
    txt=txt+"versicolor"
plt.text(3,0.5, f"largeur : {largeur} cm longueur : {longueur} cm", fontsize=12)
plt.text(3,0.3, f"k : {k}", fontsize=12)
plt.text(3,0.1, txt, fontsize=12)
#fin affichage résultats

plt.show()

Nous obtenons le résultat suivant (voir figure 5) :

FIGURE 5 – 3 plus proches voisins à l’aide de scikit-learn dans le cas : largeur pétale = 0,75 cm ; longueur pétale = 2,5 cm

Il est ensuite possible de demander aux élèves de m le programme ci-dessus afin d’étudier les changements induits par la
modification du paramètre k (notamment pour k=5) en gardant toujours les mêmes valeurs de largeur et de longueur (largeur pétale
= 0,75 cm ; longueur pétale = 2,5 cm).
Pour terminer, il est aussi possible de demander aux élèves de travailler avec d’autres valeurs de longueur et largeur.

Possibilité de projet
Il est possible, dans le cadre d’un projet, de faire travailler les élèves sur un autre jeu de données, par exemple, ”Prédire les survivants
du Titanic”. Le jeu de données peut être récupéré sur le site kaggle [6]. Le label est ”survivant” ou ”décédé”. Il sera nécessaire de
retravailler les données comme nous l’avons fait pour le jeu de données ”Iris” (supprimer des colonnes, encodage…). Dans ce projet
il sera possible de faire travailler les élèves sur des vecteurs d’entrée de dimension supérieure à 2 (le genre, l’âge, la classe occupée
par le passager sur le bateau, …).

voici un lien vers le projet Titanic développé par Benoit Fourlegnie:

projet titanic

NSI

Mini projet dictionnaire

10 septembre 2020 PLACE Thierry

Projet

En utilisant les connaissances acquises jusqu’à présent, vous allez écrire un programme de gestion de répertoire téléphonique.

Cahier des charges

Ce programme devra proposer le menu suivant à l’utilisateur :

0-quitter
1-écrire dans le répertoire
2-rechercher dans le répertoire

3-mettre les numéros au format internationale
Votre choix ?

Si le choix est 0 : Le programme sera stoppé.

Si le choix est 1 :

L’utilisateur devra saisir un nom ou un prénom ou 0 s’il veut terminer la saisie ( » Nom (0 pour terminer) : « ….) :

L’utilisateur entre 0 => le programme devra le renvoyer vers le menu
L’utilisateur entre un nom ou prénom => le programme devra lui demander de saisir le numéro de téléphone correspondant au nom. Une fois le numéro saisi, le programme devra lui proposer d’entrer un nouveau nom (ou 0 pour terminer)…

exemple de saisie d’un utilisateur (toto)

Si le choix est 2 :

L’utilisateur devra saisir le nom recherché ( » Entrer un nom : « ), ou le numéro de téléphone ( » Entrer un numéro : « ).

Si le nom recherché est présent dans le répertoire, le programme devra afficher » Le numéro recherché est : » suivi du numéro de téléphone correspondant au nom saisi.
Si le nom recherché est absent du répertoire, le programme devra afficher » Inconnu « .
…….

L’utilisateur est ensuite redirigé vers le menu principal.

recherche des utilisateurs (toto et titi)

Les noms, prénoms et numéros de téléphone devront être stockés dans un dictionnaire, le nom ou le prénom seront la clé et le numéro de téléphone sera la valeur associée à la clé.

Votre programme devra être composé au minimum de 3 fonctions : une fonction « menu », une fonction « lecture », et une fonction « ecriture »…….

Pensez à commenter votre programme, bien expliquer ce que doit faire vos fonctions et les différents tests que vous prévoyez.

NSI

Dictionnaires

10 septembre 2020 PLACE Thierry

Nous allons maintenant étudier un autre type abstrait de données : les dictionnaires aussi appelés tableau associatif.

On retrouve une structure qui ressemble, à première vue, beaucoup à un tableau (à chaque élément on associe un indice de position). Mais au lieu d’associer chaque élément à un indice de position, dans un dictionnaire, on associe chaque élément (on parle de valeur dans un dictionnaire) à une clef, on dit qu’un dictionnaire contient des couples clef:valeur (chaque clé est associée à une valeur). Exemples de couples clé:valeur => prenom:Kevin, nom:Durand, date-naissance:17-05-2005. prenom, nom et date sont des clés ; Kevin, Durand et 17-05-2005 sont des valeurs.

Voici les opérations que l’on peut effectuer sur le type abstrait dictionnaire :

ajout : on associe une nouvelle valeur à une nouvelle clé
modif : on modifie un couple clé:valeur en remplaçant la valeur courante par une autre valeur (la clé restant identique)
suppr : on supprime une clé (et donc la valeur qui lui est associée)
rech : on recherche une valeur à l’aide de la clé associée à cette valeur.

Exemples : Soit le dictionnaire D composé des couples clé:valeur suivants => prenom:Kevin, nom:Durand, date-naissance:17-05-2005. Pour chaque exemple ci-dessous on repart du dictionnaire d’origine :

ajout(D,tel:06060606) ; le dictionnaire D est maintenant composé des couples suivants : prenom:Kevin, nom:Durand, date-naissance:17-05-2005, tel:06060606
modif(D,nom:Dupont) ; le dictionnaire D est maintenant composé des couples suivants : prenom:Kevin, nom:Dupont, date-naissance:17-05-2005
suppr(D,date-naissance) ; le dictionnaire D est maintenant composé des couples suivants : prenom:Kevin, nom:Durand
rech(D,prenom) ; la fonction retourne Kevin

L’implémentation des dictionnaires dans les langages de programmation peut se faire à l’aide des tables de hachage. Les tables de hachages ainsi que les fonctions de hachages qui sont utilisées pour construire les tables de hachages, ne sont pas au programme de NSI. Cependant, l’utilisation des fonctions de hachages est omniprésente en informatique, il serait donc bon, pour votre « culture générale informatique », de connaitre le principe des fonctions de hachages. Voici un texte qui vous permettra de comprendre le principe des fonctions de hachages : c’est quoi le hachage . Pour avoir quelques idées sur le principe des tables de hachages, je vous recommande le visionnage de cette vidéo : wandida : les tables de hachage

Si vous avez visionné la vidéo de wandida, vous avez déjà compris que l’algorithme de recherche dans une table de hachage a une complexité O(1) (le temps de recherche ne dépend pas du nombre d’éléments présents dans la table de hachage), alors que la complexité de l’algorithme de recherche dans un tableau non trié est O(n). Comme l’implémentation des dictionnaires s’appuie sur les tables de hachage, on peut dire que l’algorithme de recherche d’un élément dans un dictionnaire a une complexité O(1) alors que l’algorithme de recherche d’un élément dans un tableau non trié a une complexité O(n).

Python propose une implémentation des dictionnaires, nous avons déjà étudié cette implémentation l’année dernière, n’hésitez pas à vous référer à la ressource proposée l’an passé : les dictionnaires en Python

Documentation Dictionnaires python

Mini projet Répertoire téléphonique

Auteur : David Roche

NSI, Langages et programmation

Révisions de Première (2 séances)

6 septembre 2020 Nicolas Maurin

Description

Un administrateur de réseau pédagogique a créé des comptes utilisateurs à partir de données issues des bases du rectorat.

Le format du fichier qu’il a ainsi récupéré est au format csv. Les utilisateurs sont classés par ordre alphabétique.

L’administrateur, par soucis de simplification, souhaite disposer d’un fichier csv par classe, avec les utilisateurs de cette classe par ordre alphabétique.

On vous demande de créer un programme python qui permettra ce traitement. Dans les fichiers de classe, on retrouvera les mêmes champs que dans le fichier original. Chaque fichier créé contiendra les noms des utilisateurs triés par ordre alphabétique.

Exemple à partir du fichier « utilisateurs_simple.csv » :

Le programme devra créer 3 fichiers : « 1RICIMTB.csv » – « 1TMA .csv » – « 1UFA.csv » contenant chacun les utilisateurs de la classe correspondante, classés dans l’ordre alphabétique.

1CAPT.csv

Fichier de tous les utilisateurs :

utilisateurs Télécharger

Fichier simplifié des utilisateurs (pour mise au point) :

utilisateurs_simple Télécharger

Pour aller plus loin…

Le fichier original est sous la forme suivante (image ci-dessous). Les champs sont différemment organisés et les noms d’utilisateurs ne sont pas classés dans l’ordre alphabétique. Il s’agira donc de les classer par ordre alphabétique dans les fichiers de classe…z

Fichier_utilisateurs_melanges Télécharger

Ressource :

« Utilisation du module csv dans Python » (issu du site https://pythonforge.com/module-csv-lire-ecrire/)

Utilisation_du_module_csv_Python_v22-1 Télécharger

SNT, La photographie numérique

caractéristiques d’une image numérique

16 février 2020 Erika Follien

Avant tout, créer un répertoire « thème Photo » dans votre zone personnelle SNT.

Ajouter dans ce répertoire, un nouveau dossier appelé « travail » dans lequel vous enregistrerez toutes les étapes intermédiaires de vos travaux sur les images.

Pour ce thème et les suivants, vous devez progresser sur la mise en forme de votre CR. La mise en forme sera prise en compte dans l’évaluation. Pistes de progrès à respecter:

Rédaction sans fautes d’orthographe
Utiliser l’option Justifier le texte dans LibreOffice pour utiliser toute la largeur de la page (disponible avec marge gauche, droite ou centrer)
Utiliser l’option Rogner les images afin de ne montrer que l’essentiel de la copie d’écran que vous faites
Après Rogner penser à agrandir les images pour plus de lisibilité et éventuellement centrer les images
Utiliser les options classiques de mise en forme du texte: police de caractères, titre , gras , italique , couleur , taille , souligné pour mettre en évidence les différents corps de votre texte

Une image numérique est un tableau (=matrice) de pixels. Un pixel (Picture Element) est un carré élémentaire de l’image.

A faire vous-même 1

Ouvrez le logiciel Photofiltre puis ouvrez l’image carreblanc.png (Fichier>Ouvrir) ci-dessous.

carré-blanc Télécharger

Utilisez le scroll ou l’outil zoom pour grossir l’image au maximum.
Utilisez le plus petit outil pinceau (taille 1 pixel) pour dessiner en noir l’initiale de votre prénom

Enregistrer votre image sous le nom de fichier initiale1.png.

Une image est caractérisée par différents paramètres (revoir la vidéo si besoin) : la définition, la résolution, la taille.

A faire vous-même 2

Quelles sont les caractéristiques de l’image ? Fichier>Propriétés de l’image

quelle est sa définition ?
combien de pixels contient l’image initiale1.png ?
quelle est la taille réelle de l’image ?
quelle est sa résolution ?
vérifiez par le calcul la résolution indiquée.

pour vous aider allez voir ici.

vidéo à regarder tout sur la résolution.

rappels : la résolution s’exprime en français en ppp (= pixel par pouce) ou en anglais en dpi (=dot per inch)

1 pouce (1 inch en anglais) = 2,54 cm

Si on fait varier le nombre de pixels, on modifie certains paramètres de l’image :

A faire vous-même 3

Menu Affichage > afficher la grille de repérage

Menu Outils > Préférences > palette d’outils et grille

Modifiez les paramètres de grille tels que figurés sur l’image :

Vous obtenez un quadrillage par pixels en rouge sur votre image.

Vérifiez la définition de votre image et faites une copie d’écran à joindre au compte-rendu.
Chaque pixel est codé avec 1 bit qui peut prendre 2 valeurs : noir ou blanc. Comme un octet = 8 bits, quel est le poids théorique de cette image ?
Quel serait le poids de l’image si c’était juste un carré blanc ?

A faire vous-même 4

Modifiez à nouveau les paramètres de grille de façon à quadriller avec des carrés de 2×2 pixels.
Coloriez entièrement en noir chaque carré contenant au moins 1 pixel noir.
Enregistrez la nouvelle image sous le nom initiale2.png . Faites une copie d’écran à joindre au compte-rendu.

Si on considère que chaque carré de la nouvelle grille représente un pixel :

combien de pixels contient la nouvelle version de l’image ?
quelle est sa définition ?
la taille de l’image a-t-elle changé ?
quelle est alors sa résolution ?
quel est le poids de cette nouvelle version ?

A faire vous-même 5

application

J’ai une photo dont la définition est de 3000 × 4000, la résolution est de 72 dpi. Quelle est la taille d’impression ?
Je souhaite pouvoir l’imprimer en format 10 × 13.5 cm, donc réduire les dimensions tout en gardant le même nombre de pixels. Comment puis-je faire ? L’image sera-t-elle de bonne qualité ? Quelle est maintenant la nouvelle résolution ?

NSI

Codage – Exercices

20 janvier 2020 Nicolas Maurin

Exercice 1

Ecrire une fonction decimal_vers_binaire() qui prend comme argument un nombre entier décimal saisi par l’utilisateur et qui renvoi le nombre binaire correspondant sur 1 octet (8bits).

La fonction devra coder le nombre décimal en binaire et rajoutera le nombre de 0 voulu pour faire un octet.

Exemples :

Exercice 2

Modifier la fonction précédente pour coder le nombre entier sur 16 bits.

Exemples :

Exercice 3

Ecrire une fonction plus_un() qui ajoute 1 à un nombre binaire de 8 bits saisi par l’utilisateur passé en argument.

Exemples :

Pour vous aiguiller :
1- Recopier l’octet saisi par l’utilisateur dans une liste.
2- Comparer chaque bit, rang par rang. Si le bit de rang 0 est égal à 1, le changer à 0 et marquer la retenue à Vraie. Si le bit de rang 0 est égal à 0, le changer à 1 et garder les autres intacts.
3- Si la retenue est Vraie tester les bit de rang suivant, les uns après les autres tant que la retenue est Vraie.
4- Recopie du résultat dans un string que l’on affichera en appelant la fonction plus_un()

Exercice 4

Ecrire un programme qui permet de convertir les nombres entiers en binaire signé en complément à 2 (en 8 bits) .
1- Adapter la fonction decimal_vers_binaire () de l’exercice 1 afin de convertir le nombre binaire en décimal (sur 7 bits).
2- Créer une fonction inversion() qui prend en argument le nombre binaire convertit précédemment et renvoi le résultat d’une inversion bit à bit.
3- Utiliser la fonction plus_un() de l’exercice 3 avec comme argument le nombre binaire renvoyé par la fonction inversion() et renvoi le résultat de l’addition de ce dernier avec 1.
Enfin, imprimer à l’écran le résultat et vérifier la justesse de ce dernier.

Exemples :

Exercice 5

NoteBook de correction

NSI

Linux : les commandes de base en ligne de commande

9 janvier 2020 PLACE Thierry

À la « préhistoire » des systèmes d’exploitation, ces derniers étaient dépourvus d’interface graphique (système de fenêtres « pilotables » à la souris), toutes les interactions « système d’exploitation – utilisateur » se faisaient par l’intermédiaire de « lignes de commandes » (suites de caractères, souvent ésotériques, saisies par l’utilisateur). Aujourd’hui, même si les interfaces graphiques modernes permettent d’effectuer la plupart des opérations, il est important de connaitre quelques-unes de ces lignes de commandes.

Nous allons utiliser une clé Freeduc-JBART, cette clé est basée sur Debian-Live , ce qui nous permettra de travailler sous Linux .

Pour saisir des lignes de commandes, nous allons utiliser une console (aussi appelé terminal même si ce n’est pas exactement la même chose).

À faire vous-même 1

Après avoir démarrer sur votre clé Freeduc-JBART

Ouvrez une console, vous devriez avoir quelque chose qui ressemble à cela :

console système GNU/Linux

Nous avons ci-dessus la console de l’utilisateur « david » qui utilise un ordinateur qui se nomme « PC-Bureau » (« david@PC-Bureau »).

Principalement nous allons, grâce à la ligne de commande, travailler sur les fichiers et les répertoires. Dans les systèmes de type « UNIX » (par exemple GNU/Linux ou macOS), nous avons un système de fichier en arborescence :

système de fichiers

Dans le schéma ci-dessus on trouve des répertoires (noms entourés d’un rectangle, exemple : « home ») et des fichiers (uniquement des noms « grub.cfg »). À noter : les extensions des noms de fichiers, par exemple le « cfg » de « grub.cfg », ne sont pas obligatoires dans les systèmes de type « UNIX », par exemple, « bash » est bien un nom de fichier et il n’a pas d’extension.

On parle d’arborescence, car ce système de fichier ressemble à un arbre à l’envers.

Comme vous pouvez le constater, la base de l’arbre s’appelle la racine de l’arborescence et se représente par un « / »

Chemin absolu ou chemin relatif ?

Pour indiquer la position d’un fichier (ou d’un répertoire) dans l’arborescence, il existe 2 méthodes : indiquer un chemin absolu ou indiquer un chemin relatif. Le chemin absolu doit indiquer « le chemin » depuis la racine. Par exemple le chemin absolu du fichier fiche.ods sera : /home/elsa/documents/fiche.ods

Remarquez que nous démarrons bien de la racine / (attention les symboles de séparation sont aussi des /)

Il est possible d’indiquer le chemin non pas depuis la racine, mais depuis un répertoire quelconque, nous parlerons alors de chemin relatif :

Le chemin relatif permettant d’accéder au fichier « photo_1.jpg » depuis le répertoire « max » est : « images/photo_vac/photo_1.jpg »

Remarquez l’absence du / au début du chemin (c’est cela qui nous permettra de distinguer un chemin relatif et un chemin absolu).

Imaginons maintenant que nous désirions indiquer le chemin relatif pour accéder au fichier « gdbd_3.jpg » depuis le répertoire « photos_vac ».

Comment faire ?

Il faut « remonter » d’un « niveau » dans l’arborescence pour se retrouver dans le répertoire « images » et ainsi pouvoir repartir vers la bonne « branche ». Pour ce faire il faut utiliser 2 points : ..

« ../ski/gdbd_3.jpg »

Il est tout à fait possible de remonter de plusieurs « crans » : « ../../ » depuis le répertoire « photos_vac » permet de « remonter » dans le répertoire « max »

À faire vous-même 2

En vous basant sur l’arborescence ci-dessus, déterminez le chemin absolu permettant d’accéder au fichier :

« cat »
« rapport.odt »

Toujours en vous basant sur l’arborescence ci-dessus, déterminez le chemin relatif permettant d’accéder au fichier :

« rapport.odt » depuis le répertoire « elsa »
« fiche.ods » depuis le répertoire « boulot »

Comme déjà évoqué plus haut, les systèmes de type « UNIX » sont des systèmes « multi-utilisateurs » : chaque utilisateur possède son propre compte. Chaque utilisateur possède un répertoire à son nom, ces répertoires personnels se situent traditionnellement dans le répertoire « home ». Dans l’arborescence ci-dessus, nous avons 2 utilisateurs : « max » et « elsa ». Par défaut, quand un utilisateur ouvre une console, il se trouve dans son répertoire personnel. Dans l’image de la console ci-dessus, nous avons un « david@PC-Bureau ~ $ » (au passage, on appelle cela « l’invite de commande »), le « ~ » (caractère « tilde ») signifie que l’on se trouve actuellement dans le répertoire personnel de l’utilisateur courant, autrement dit dans le répertoire de chemin absolu « /home/david » (puisque l’utilisateur courant est « david »). Le répertoire « où l’on se trouve actuellement » est appelé « répertoire courant ». L’invite de commande vous indique à tout moment le répertoire courant : « david@PC-Bureau ~/Documents $ » vous indique que vous êtes dans le répertoire « Documents » qui se trouve dans le répertoire « david » qui se trouve dans le répertoire « home » (chemin absolu : « /home/david/Documents »)

Attention : les systèmes de type « UNIX » sont « sensibles à la casse » (il faut différencier les caractères majuscules et les caractères minuscules) : le répertoire « Documents » et le répertoire « documents » sont 2 répertoires différents.

La commande cd

Signification : list

La commande « cd » permet de changer le répertoire courant. Il suffit d’indiquer le chemin (relatif ou absolu) qui permet d’atteindre le nouveau répertoire :

Par exemple (en utilisant l’arborescence ci-dessus) :

si le répertoire courant est le répertoire « elsa » et que vous « voulez vous rendre » dans le répertoire « documents », il faudra saisir la commande : « cd documents » (relatif) ou « cd /home/elsa/documents » (absolu)
si le répertoire courant est le répertoire « photos_vac » et que vous « voulez vous rendre » dans le répertoire « ski », il faudra saisir la commande : « cd ../ski » (relatif) ou « cd /home/max/images/ski » (absolu)
si le répertoire courant est le répertoire « boulot » et que vous « voulez vous rendre » dans le répertoire « documents », il faudra saisir la commande : « cd .. » (relatif) ou « cd /home/elsa/documents » (absolu)

À faire vous-même 3

Toujours en utilisant l’arborescence ci-dessus, quelle est la commande à saisir si le répertoire courant est le répertoire « home » et que vous « voulez vous rendre » dans le répertoire « boulot » (vous utiliserez d’abord un chemin absolu puis un chemin relatif)

La commande ls

Signification : list

La commande « ls » permet de lister le contenu du répertoire courant.

Dans l’exemple ci-dessus, depuis le répertoire personnel de l’utilisateur « david », nous passons dans le répertoire « nsi » à l’aide d’un « cd nsi », puis nous affichons le contenu de ce répertoire « nsi » à l’aide de la commande « ls ». Nous trouvons dans le répertoire « nsi » : 2 fichiers (« fiche1.odt » et « photo.jpg ») et un répertoire (« test »).

À faire vous-même 4

Après avoir ouvert une console, utilisez la commande ls depuis votre répertoire personnel.

La commande « mkdir »

Signification : make directory

La commande « mkdir » permet de créer un répertoire dans le répertoire courant. La commande est de la forme « mkdir nom_du_répertoire »

Remarque : il est préférable de ne pas utiliser de caractères accentués dans les noms de répertoire (ou de fichier). Il en est de même pour les espaces (à remplacer par des caractères tirets bas « _ »)

La commande man

Signification : manual

Affiche les pages du manuel système.
Chaque argument donné à man est généralement le nom d’un programme, d’un utilitaire, d’une fonction ou d’un fichier spécial. Exemples d’utilisation :

man man
affiche les informations pour l’utilisation de man
man mkdir
affiche les informations pour l’utilisation de mkdir

‘q’ pour quitter.

À faire vous-même 5

Après avoir ouvert une console, utilisez la commande « mkdir » afin de créer un répertoire « test_nsi » dans votre répertoire personnel.

La commande « rm »

Signification : remove

La commande « rm » permet de supprimer un fichier ou un répertoire. La commande est de la forme « rm nom_du_répertoire_ou_nom_du_fichier »

La plupart des commandes UNIX peuvent être utilisées avec une ou des options. Par exemple, pour supprimer un répertoire non vide, il est nécessaire d’utiliser la commande « rm » avec l’option « -r » : « rm -r nom_du_répertoire »

Attention si vous utilisez la commande « rm * » cela supprime tous les fichiers présent dans le répertoire courant.

A noter que pour afficher le répertoire courant il existe une fonction « pwd », même s’il est spécifié sur le terminal en bleu…

La commande « touch »

La commande « touch » permet de créer un fichier vide. La commande est de la forme « touch nom_du_fichier_à_créer »

La commande « cp »

Signification : copy

La commande « cp » permet de copier un fichier. La commande est de la forme « cp /répertoire_source/nom_fichier_à_copier /répertoire_destination/nom_fichier »

À noter : le nom du fichier « destination » n’est pas obligatoirement le même que le nom du fichier « source » (on peut avoir « cp fic.txt info/fiche.txt »)

La commande « mv »

Signification : move

la commande « mv » permet de déplacer ou renommer des fichiers et des répertoires Options les plus fréquentes :

-f : Écrase les fichiers de destination sans confirmation
-i : Demande confirmation avant d’écraser
-u : N’écrase pas le fichier de destination si celui-ci est plus récent

Exemples d’utilisation :

mv monFichier unRep/
Déplace monFichier dans le répertoire unRep
mv unRep/monFichier .
Déplace le fichier monFichier du répertoire unRep là où on se trouve
mv unRep monRep
Renomme unRep en monRep

À faire vous-même 6

Placez-vous dans le répertoire « test_nsi » créé au « À faire vous-même 5 ». Créez un fichier « test.txt » avec du texte à l’intérieur.

Saisir la commande « cat test.txt » que se passe t’il?

Créez un répertoire « doc ». Copiez le fichier « test.txt » dans le répertoire « doc ». Effacez le répertoire doc (et son contenu).

Gestion des utilisateurs et des groupes

Les systèmes de type « UNIX » sont des systèmes multi-utilisateurs, plusieurs utilisateurs peuvent donc partager un même ordinateur, chaque utilisateur possédant un environnement de travail qui lui est propre.

Chaque utilisateur possède certains droits lui permettant d’effectuer certaines opérations et pas d’autres. Le système d’exploitation permet de gérer ces droits très finement. Un utilisateur un peu particulier est autorisé à modifier tous les droits : ce « super utilisateur » est appelé « administrateur » ou « root ». L’administrateur pourra donc attribuer ou retirer des droits aux autres utilisateurs. Au lieu de gérer les utilisateurs un par un, il est possible de créer des groupes d’utilisateurs. L’administrateur attribue des droits à un groupe au lieu d’attribuer des droits particuliers à chaque utilisateur.

Comme nous venons de le voir, chaque utilisateur possède des droits qui lui ont été octroyés par le « super utilisateur ». Nous nous intéresserons ici uniquement aux droits liés aux fichiers, mais vous devez savoir qu’il existe d’autres droits liés aux autres éléments du système d’exploitation ((imprimante, installation de logiciels…).

Les fichiers et les répertoires possèdent 3 types de droits :

les droits en lecture (symbolisés par la lettre r) : est-il possible de lire le contenu de ce fichier
les droits en écriture (symbolisés par la lettre w) : est-il possible de modifier le contenu de ce fichier
les droits en exécution (symbolisés par la lettre x) : est-il possible d’exécuter le contenu de ce fichier (quand le fichier du code exécutable)

Il existe 3 types d’utilisateurs pour un fichier ou un répertoire :

le propriétaire du fichier (par défaut c’est la personne qui a créé le fichier), il est symbolisé par la lettre u
un fichier est associé à un groupe, tous les utilisateurs appartenant à ce groupe possèdent des droits particuliers sur ce fichier. Le groupe est symbolisé par la lettre g
tous les autres utilisateurs (ceux qui ne sont pas le propriétaire du fichier et qui n’appartiennent pas au groupe associé au fichier). Ces utilisateurs sont symbolisés la lettre « o »

Il est possible d’utiliser la commande « ls » avec l’option « -l » afin d’avoir des informations supplémentaires.

Prenons la première ligne :


-rw-r--r-- 1 david david 0 avril 13 19:58 fic.txt

Lisons cette ligne de gauche à droite :

le premier symbole « – » signifie que l’on a affaire à un fichier, dans le cas d’un répertoire, nous aurions un « d » (voir la 2e ligne)
les 3 symboles suivants « rw-« donnent les droits du propriétaire du fichier : lecture autorisée (r), écriture autorisée (w), exécution interdite (- à la place de x)
les 3 symboles suivants « r–« donnent les droits du groupe lié au fichier : lecture autorisée (r), écriture interdite (- à la place de w), exécution interdite (- à la place de x)
les 3 symboles suivants « r–« donnent les droits des autres utilisateurs : lecture autorisée (r), écriture interdite (- à la place de w), exécution interdite (- à la place de x)
le caractère suivant « 1 » donne le nombre de liens (nous n’étudierons pas cette notion ici)
le premier « david » représente le nom du propriétaire du fichier
le second « david » représente le nom du groupe lié au fichier
le « 0 » représente la taille du fichier en octet (ici notre fichier est vide)
« avril 13 19:58 » donne la date et l’heure de la dernière modification du fichier
« fic.txt » est le nom du fichier

Prenons la deuxième ligne :


drwxr-xr-x 2 david david 4096 avril 13 20:05 info

Lisons cette ligne de gauche à droite :

le premier symbole « d » signifie que l’on a un répertoire
les 3 symboles suivants « rwx »donnent les droits du propriétaire du répertoire : lecture du contenu du répertoire autorisée (r), modification du contenu du répertoire autorisée (w), il est possible de parcourir le répertoire (voir le contenu du répertoire) (x)
les 3 symboles suivants « r-x »donnent les droits du groupe lié au répertoire : modification du contenu du répertoire interdite (- à la place de w)
les 3 symboles suivants « r-x »donnent les droits des autres utilisateurs : modification du contenu du répertoire interdite (- à la place de w)
le caractère suivant « 2 » donne le nombre de liens (nous n’étudierons pas cette notion ici)
le premier « david » représente le nom du propriétaire du répertoire
le second « david » représente le nom du groupe lié au répertoire
le « 4096 » représente la taille du répertoire en octets
« avril 13 20:05 » donne la date et l’heure de la dernière modification du contenu du répertoire
« info » est le nom du répertoire

À faire vous-même 7

Analysez la 3e ligne du résultat de la commande « ls -l » ci-dessus

Il est important de ne pas perdre de vu que l’utilisateur « root » a la possibilité de modifier les droits de tous les utilisateurs.

Le propriétaire d’un fichier peut modifier les permissions d’un fichier ou d’un répertoire à l’aide de la commande « chmod ». Pour utiliser cette commande, il est nécessaire de connaitre certains symboles :

les symboles liés aux utilisateurs : « u » correspond au propriétaire, « g » correspond au groupe lié au fichier (ou au répertoire), « o » correspond aux autres utilisateurs et « a » correspond à « tout le monde » (permet de modifier « u », « g » et « o » en même temps)
les symboles liés à l’ajout ou la suppression des permissions : « + » on ajoute une permission, « – » on supprime une permission, « = » les permissions sont réinitialisées (permissions par défaut)
les symboles liés aux permissions : « r » : lecture, « w » : écriture, « x » : exécution.

La commande « chmod » à cette forme :


chmod [u g o a] [+ - =] [r w x] nom_du_fichier

par exemple


chmod o+w toto.txt

attribuera la permission « écriture » pour le fichier « toto.txt » « aux autres utilisateurs »

Il est possible de combiner les symboles :


chmod g-wx toto.txt

La commande « chmod » ci-dessus permet de supprimer la permission « écriture » et la permission « exécution » pour le fichier « toto.txt » « au groupe lié au fichier »

Une fois de plus, « root » a tous les droits sur l’ensemble des fichiers et des répertoires, il peut donc utiliser la commande « chmod » sur tous les répertoires et tous les fichiers.

À faire vous-même 8

Analysez attentivement l’enchainement de commandes suivantes :

À faire vous-même 9

Créez un répertoire « test_nsi2 » dans votre répertoire personnel. Placez-vous dans le répertoire « test_nsi2 ». Créez un fichier « titi.txt », vérifiez les permissions associées à ce fichier. Modifiez les permissions associées au fichier « titi.txt » afin que les « autres utilisateurs » aient la permission « écriture »

Retrouver toutes les commandes ici : documentation Ubuntu console de commande

NSI

Extraction de données d’un fichier csv et tri simple sur une liste

12 décembre 2019 PLACE Thierry

Présentation

On se propose dans cette activité de traiter des données issues d’un fichier csv récupéré sur le site Strava afin de les filtrer dans un nouveau fichier.
Le fichier de données de départ se nomme « liste_origine.csv ».

liste_origine Télécharger

Il faudra écrire 5 fonctions :
• « import_lignes » avec en argument le fichier de données de départ et qui renvoie une liste des lignes contenues dans le fichier.
• « Separe_lignes » avec en argument la liste précédente et qui renvoie la liste avec les lignes séparées.
• « creation_liste » qui créera la liste voulue en enlevant les champs inutiles.
• « classement_annee » permettra de ne garder que les lignes de l’année courante.
• « nouveau_fichier » qui écrira les lignes de l’année dans un nouveau fichier créé pour l’occasion.

Activité 1 : Présentation et découverte du format csv

Strava est un site qui est utilisé pour enregistrer des activités sportives. Les membres du site peuvent partager leurs activités préalablement enregistrées via GPS. En cyclisme et en course à pied, il existe des segments de route chronométrés où les athlètes peuvent se concurrencer. Nous travaillerons sur un fichier contenant les performances d’une montée du Mont-Ventoux, réalisée en cyclisme.
Les données sont alors disponibles et téléchargeables dans un fichier au format csv. Un fichier csv est un fichier texte, représentant des données tabulaires sous forme de valeurs séparées par des virgules, tabulations ou points-virgules. Les lignes sont séparées par un retour à la ligne matérialisé par un « \n ».

Dans notre cas, ouvrir le fichier « liste_origine.csv » avec un éditeur de texte, et indiquer quel est le séparateur utilisé :
Séparateur : ?
Quels champs (étiquettes des colonnes) contient-il ?
?
Nous souhaitons traiter ce fichier, en ne gardant uniquement que les performances de l’année en cours et en séparant le nom du prénom car dans le champ « nom » il y a les 2, mais également en supprimant les champs qui ne nous intéressent pas (« Vitesse », « HR », « Puissance », « Vit. Ascens. » et « Temps »)
Pour cela, il faudra dans un premier temps récupérer les lignes contenues dans le fichier de départ et les placer dans une liste exploitable.

Activité 2 : Récupération des lignes du fichier de départ

Écrire une fonction « import_lignes » qui prend en argument un nom de fichier (on testera avec le nôtre « liste_origine.csv ») et qui renvoie la liste des lignes du fichier, c’est-à-dire une liste de chaînes de caractères, où chaque élément de la liste correspond à une ligne du fichier. Il faudra bien penser à fermer le fichier avant de faire le return ! Tester votre fonction en affichant le résultat de la liste créée.

un peu d’aide fiche

Lecture_ecriture_fichier Télécharger

et toujours fiche mémo

ficheMémo_python Télécharger

Activité 3 : Séparation des lignes

Écrire une fonction « separe_lignes » qui prend en argument une chaine de caractère et qui renvoie une liste contenant les chaînes de caractères correspondants aux champs de notre fichier.

(par exemple: separe_lignes(’28;David POLVERONI;21/09/2012;17,7km/h;166bpm;300W;1368,0;01:05:56;3956\n’) renvoie une liste =[’28’, ‘David POLVERONI’, ’21/09/2012′, ‘17,7km/h’, ‘166bpm’, ‘300W’, ‘1368,0’, ’01:05:56′, ‘3956’] Elle sera obtenue en séparant la ligne le long des points-virgules. Pour cela, aidez-vous de la propriété « chaine_caractere.strip » qui permet d’enlever un éventuel \n (retour à la ligne) et/ou des espaces à la fin de la chaine de caractère, ainsi que de la propriété » chaine_caractere .split(« ; ») » qui sépare la ligne à chaque fois qu’un point-virgule est rencontré…

aide sur les méthodes s’appliquant au string w3schools

Activité 4 : Création d’un dictionnaire dico_coureur

Écrire une fonction « creation_dico » qui prend en argument une ligne (chaîne de caractères) et qui renvoie un dictionnaire correspondant au cycliste de la ligne, en omettant les champs non retenus (« Vitesse », « HR », « Puissance », « Vit. Ascens. » et « Temps »)…
Exemple de résultat : creation_dico(‘2;Romain Bardet;17/06/2019;19,9km/h;-;-;1\xa0539,7;00:58:35;3515\n’) doit renvoyer : {‘classement’: ‘2’, ‘nomcomplet’: ‘Romain Bardet’, ‘date’: ’17/06/2019′, ‘temps_s’: ‘3515’} , si vous voulez séparer la clé nomcomplet en deux clé prenom et nom.

Activité 5 : Création d’une liste de dictionnaire

Écrire une fonction « liste_perf » qui prend en argument un nom de fichier et qui renvoie une liste de dictionnaire des performances correspondant aux lignes du fichier ( en omettant la première ligne).

Exemple de résultat: liste_perf (‘liste_origine.csv’) doit renvoyer : une liste de dictionnaire:

[{‘classement’: ‘1’, ‘nomcomplet’: ‘Laurens ten Dam’, ‘date’: ’14/07/2013′, ‘temps_s’: ‘3497’}, {‘classement’: ‘2’, ‘nomcomplet’: ‘Romain Bardet’, ‘date’: ’17/06/2019′, ‘temps_s’: ‘3515’}, {‘classement’: ‘3’, ‘nomcomplet’: ‘Rein Taaramae’, ‘date’: ’17/06/2019′, ‘temps_s’: ‘3583’}, {‘classement’: ‘4’, ‘nomcomplet’: ‘El Fares Julien’, ‘date’: ’17/06/2019′, ‘temps_s’: ‘3607’},…… , {‘classement’: ’28’, ‘nomcomplet’: ‘David POLVERONI’, ‘date’: ’21/09/2012′, ‘temps_s’: ‘3956’}]

Activité 6 : Création d’une liste de dictionnaire

Écrire une fonction « classement_annee » qui prend en argument la liste de dictionnaire précédemment créée et qui renvoie une nouvelle liste contenant uniquement les performances de l’année 2019. Pour cela, vous devrez vous aider de la liste créer lors de l’activité précédente , pour rechercher l’année dans la date vous devrez utiliser la propriété .split(‘/’), vue précédemment !
Exemple de résultat : classement_annee([{‘classement’: ‘1’, ‘prenom’: ‘Laurens’, ‘nom’: ‘ten’, ‘date’: ’14/07/2013′, ‘temps_s’: 3497}, {‘classement’: ‘2’, ‘prenom’: ‘Romain’, ‘nom’: ‘Bardet’, ‘date’: ’17/06/2019′, ‘temps_s’: 3515}])

doit renvoyer : [{‘classement’: ‘2’, ‘prenom’: ‘Romain’, ‘nom’: ‘Bardet’, ‘date’: ’17/06/2019′, ‘temps_s’: 3515]

Si vous voulez vous pouvez ajouter l’année de tri en argument, et trié ainsi en fonction de l’année donnée en argument.

Pour aller plus loin : Écriture dans un nouveau fichier

On souhaite enfin réécrire tous ces résultats dans un nouveau fichier « classement_2019.csv ». Pour cela, écrire une fonction « nouveau_fichier » qui prend en argument la liste précédente et qui va l’écrire ligne à ligne dans le fichier « classement_2019.csv » en insérant des points-virgules entre les champs. La première ligne du fichier devra être : » ‘classement;prenom;nom;date;temps_s;’+’\n’ «

extrac_csv Télécharger

NSI

Exercice 3 : Dictionnaire

16 octobre 2019 icnisnboissy

Stock de fruits

Dans cet exercice, nous allons gérer un stock de fruits qui sera représenté par un dictionnaire, dont les clés seront les noms de fruits (au singulier), et les valeurs seront le nombre de fruits correspondant dans le stock. Par exemple, si le stock contient 2 pommes et 6 bananes, il sera représenté par le dictionnaire suivant: {‘pomme’ : 2, ‘banane’ : 6}. Pour simplifier l’écriture des exemples, on supposera que ce dictionnaire sera stocké dans une variable appelée stock.

Dans tout l’exercice, le(s) dictionnaire(s) passé(s) en argument ne doi(ven)t pas être modifié(s).

Vous n’êtes pas obligés de traiter les questions dans l’ordre.

Ecrire une fonction ajoute1 qui prend en argument un stock (dictionnaire) et un nom de fruit, et qui renvoie le nouveau stock, dans lequel un fruit du type donné a été ajouté.
Test:
- ajoute1(stock , 'pomme') renvoie {'pomme' : 3, 'banane' : 6}
- ajoute1(stock , 'poire') renvoie {'pomme' : 2, 'banane' : 6, 'poire' : 1}
Ecrire une fonction enleve1 qui prend en argument un stock (dictionnaire) et un nom de fruit, et qui renvoie le nouveau stock, où un fruit du type donné a été enlevé (s’il y avait un stock suffisant). Si le stock de ce fruit tombe à zéro, il faut enlever la clé du dictionnaire. Si le stock n’était pas suffisant, le programme affichera « Erreur: quantité insuffisante de (*nom du fruit*) » et renverra le stock initial non modifié.
Test:
- enleve1(stock , 'pomme') renvoie {'pomme' : 1, 'banane' : 6}
- enleve1(stock , 'poire') affiche « Erreur: Quantité insuffisante de poire » et renvoie {‘pomme’ : 2, ‘banane’ : 6}
Ecrire une fonction ajoute qui prend en argument un stock (dictionnaire), un nom de fruit et une quantité q, et qui renvoie le nouveau stock, dans lequel on a ajouté une quantité q du type de fruit précisé.
Test:
- ajoute(stock , 'pomme', 5) renvoie {‘pomme’ : 7, ‘banane’ : 6}
- ajoute(stock , 'poire', 4) renvoie {‘pomme’ : 2, ‘banane’ : 6, ‘poire’ : 4}
Ecrire une fonction enleve qui prend en argument un stock (dictionnaire), un nom de fruit et une quantité q, et qui renvoie le nouveau stock où l’on a enlevé la quantité q du type de fruit précisé. De même que pour la fonction enleve1, si le stock de ce fruit tombe à zéro, il faut enlever la clé du dictionnaire. Si le stock n’était pas suffisant, le programme affichera « Erreur: quantité insuffisante de (*nom du fruit*) » et renverra le stock initial non modifié.
Test:
- enleve(stock , 'pomme', 2) renvoie {'banane' : 6}
- enleve(stock , 'banane', 10) affiche « Erreur: Quantité insuffisante de banane » et renvoie {‘pomme’ : 2, ‘banane’ : 6}
Ecrire une fonction apres_livraison qui prend en argument un stock (dictionnaire) ainsi que le contenu de la livraison (représenté aussi par un dictionnaire) et qui renvoie le nouveau stock après la livraison.
Test:
- apres_livraison(stock , {'peche' : 4, 'pomme' : 5}) renvoie {‘pomme’ : 7, ‘banane’ : 6, ‘peche’ : 4}
Ecrire une fonction commande qui prend en argument le stock actuel (dictionnaire) ainsi que le stock minimum voulu (dictionnaire aussi) et qui renvoie le dictionnaire correspondant à la commande qu’il faut faire pour obtenir le stock voulu. Si le fruit apparaît déjà en quantité suffisante dans le stock actuel (supérieure ou égal au stock voulu), il ne doit pas apparaître dans la commande.
Test:
- En supposant que stock_voulu={'pomme': 15, 'orange': 20}, alors commande(stock , stock_voulu) renvoie {‘pomme’ : 13, ‘orange’ : 20}.
- En supposant que stock_voulu={'pomme': 10, 'banane': 4}, alors commande(stock , stock_voulu) renvoie {‘pomme’ : 8}.
Ecrire une fonction total qui prend en argument le stock et qui renvoie le nombre total de fruits présents dans le stock (tous types confondus)
Test:
- total(stock) renvoie 8.
Ecrire une fonction quantite qui prend en argument le stock ainsi qu’une liste de noms de fruits fruits_a_compter, et qui renvoie la quantité de fruits présents dans le stock dont le nom est dans la liste fruits_a_compter.
Test:
- En supposant que stock_bis={'pomme': 15, 'peche': 4, 'citron': 3, 'orange': 20}, alors quantite(stock_bis , ['pomme', 'citron', 'poire']) renvoie 18.
Ecrire une fonction quantite_agrumes qui prend en argument le stock et qui renvoie la quantité d’agrumes présents dans le stock. Seront considérés comme noms d’agrumes: orange, citron, mandarine, clémentine (sans accent dans le code) et pamplemousse.
Test:
- En supposant que stock_bis={'pomme': 15, 'peche': 4, 'citron': 3, 'orange': 20}, alors quantite_agrumes(stock_bis) renvoie 23.