Archives de catégorie : PROJET
Morpion
description du projet sur colab:
Tri-fusion
Etudions d’abord l’algorithme de la fusion de 2 listes:
FUSIONNER (`liste_gauche`, `liste_droite`):
* On parcourt les deux listes `gauche` et `droite` en même temps,
Pour chaque paire d’éléments, on place le plus petit dans liste resultat.
* S’il reste des éléments dans `gauche` ou dans `droite` on les place à la fin de liste resultat
Développement graphique:
Soit 2 listes à fusionner:
Liste gauche : [3, 1, 4, 7, 8] et la liste droite : [2, 5, 6]



implémenter sous pyzo la fonction FUSIONNE donc voici le début:
def fusionne(lst1, lst2):
"""
list1 est une liste
list2 est une liste
la fonction retourne une liste resultat fusion des 2 listes list1 et list2
Example
-------
>>> fusionne([3, 1, 4, 7, 8], [2, 5, 6])
# listes non ordonnées
[2, 3, 1, 4, 5, 6, 7, 8]
>>> fusionne([1, 3, 4, 7, 8], [2, 5, 6])
# listes ordonnées
[1, 2, 3, 4, 5, 6, 7, 8]
"""Maintenant regardons l’algorithme de la fonction TRI FUSION
TRI FUSION (liste):
• Si liste est de taille <= 1 on ne fait rien.
• Sinon, On sépare liste en 2 parties gauche et droite,
• On appelle Tri fusion sur gauche et sur droite
• On fusionne gauche et droite dans liste
Développement graphique :
Soit la liste [2, 3, 1, 4, 5, 6, 7, 8] à trier par fusion
on sépare d’abord :

et on fusionne avec la fonction FUSIONNE décrite juste avant:

implémenter cette fonction
def fusionne(lst1, lst2):
"""
list1 est une liste
list2 est une liste
la fonction retourne une liste resultat fusion des 2 listes list1 et list2
Example
-------
>>> fusionne([3, 1, 4, 7, 8], [2, 5, 6])
# listes non ordonnées
[2, 3, 1, 4, 5, 6, 7, 8]
>>> fusionne([1, 3, 4, 7, 8], [2, 5, 6])
# listes ordonnées
[1, 2, 3, 4, 5, 6, 7, 8]
"""
def tri_fusion(lst):
'''lst est une liste non triées
Elle est coupé en 2 listes gauche et droite par le milieu (ou presque si taille impaire),
puis la fonction tri_fusion est rappelée pour chaque liste gauche et droite, jusqu'à n'obtenir des listes de taille 1.
en fin on applique la fonction fusionne les listes gauche et droite dans une liste que la fonction renvoie.
Exemple:
>>> tri_fusion([2, 3, 1, 4, 5, 6, 7, 8])
[1, 2, 3, 4, 5, 6, 7, 8]'''''
voici un programme pour créer des listes triées ou aléatoire pour faire des tests:
import random
def liste_triee(nb):#Création d'une liste trièe dans l'ordre croissant de nb valeur
nmax=nb
L=[]
for i in range(0,nmax):
L.append(i)
return L
def liste_aleatoire(nb):# fabrication d'une liste de nb valeurs aléatoires
nmax=nb
L=[]
for i in range(0,nmax):
L.append(random.randint(0,nmax))
return LProjet : implémentation en Python des algorithmes sur les arbres binaires
Le but de ce projet est d’implémenter en Python les algorithmes sur les arbres binaires précédemment étudiés. Il sera donc sans doute nécessaire de reprendre ce qui a été vu sur la structure de données « arbre » et sur « les algorithmes sur les arbres binaires ».
Comme nous l’avons déjà dit, Python ne propose pas de structure de données permettant d’implémenter directement les arbres binaires. Il va donc être nécessaire de créer cette structure. Pour programmer ce type de structure, nous allons utiliser le paradigme objet (à voir si pas encore étudier paradigme objet)
Vous trouverez ci-dessous la classe « ArbreBinaire » qui va nous permettre d’implémenter des arbres binaires.
class ArbreBinaire:
def __init__(self, valeur):
self.valeur = valeur
self.enfant_gauche = None
self.enfant_droit = None
def insert_gauche(self, valeur):
if self.enfant_gauche == None:
self.enfant_gauche = ArbreBinaire(valeur)
else:
new_node = ArbreBinaire(valeur)
new_node.enfant_gauche = self.enfant_gauche
self.enfant_gauche = new_node
def insert_droit(self, valeur):
if self.enfant_droit == None:
self.enfant_droit = ArbreBinaire(valeur)
else:
new_node = ArbreBinaire(valeur)
new_node.enfant_droit = self.enfant_droit
self.enfant_droit = new_node
def get_valeur(self):
return self.valeur
def get_gauche(self):
return self.enfant_gauche
def get_droit(self):
return self.enfant_droit
À faire vous-même 1
Étudiez attentivement la classe « ArbreBinaire » (méthodes et attributs). Vous pouvez, par exemple, vous interroger sur l’utilité de toutes les méthodes de cette classe.
Voici un exemple d’utilisation de cette classe pour construire un arbre binaire :
Soit l’arbre binaire suivant : 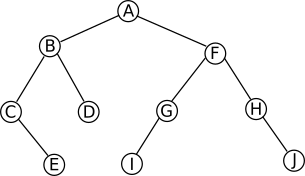 Arbre 1
Arbre 1
Voici le programme qui va permettre de construire cet arbre à l’aide de la classe « ArbreBinaire » :
class ArbreBinaire:
def __init__(self, valeur):
self.valeur = valeur
self.enfant_gauche = None
self.enfant_droit = None
def insert_gauche(self, valeur):
if self.enfant_gauche == None:
self.enfant_gauche = ArbreBinaire(valeur)
else:
new_node = ArbreBinaire(valeur)
new_node.enfant_gauche = self.enfant_gauche
self.enfant_gauche = new_node
def insert_droit(self, valeur):
if self.enfant_droit == None:
self.enfant_droit = ArbreBinaire(valeur)
else:
new_node = ArbreBinaire(valeur)
new_node.enfant_droit = self.enfant_droit
self.enfant_droit = new_node
def get_valeur(self):
return self.valeur
def get_gauche(self):
return self.enfant_gauche
def get_droit(self):
return self.enfant_droit
#######fin de la classe########
######début de la construction de l'arbre binaire###########
racine = ArbreBinaire('A')
racine.insert_gauche('B')
racine.insert_droit('F')
b_node = racine.get_gauche()
b_node.insert_gauche('C')
b_node.insert_droit('D')
f_node = racine.get_droit()
f_node.insert_gauche('G')
f_node.insert_droit('H')
c_node = b_node.get_gauche()
c_node.insert_droit('E')
g_node = f_node.get_gauche()
g_node.insert_gauche('I')
h_node = f_node.get_droit()
h_node.insert_droit('J')
######fin de la construction de l'arbre binaire###########
À faire vous-même 2
Étudiez attentivement le programme ci-dessus afin de comprendre le principe de « construction d’un arbre binaire »
Il est possible d’afficher un arbre binaire dans la console Python, pour cela, nous allons écrire une fonction « affiche ». Cette fonction renvoie une série de tuples de la forme (valeur,arbre_gauche, arbre_droite), comme « arbre_gauche » et « arbre_droite » seront eux-mêmes affichés sous forme de tuples, on aura donc un affichage qui ressemblera à : (valeur,(valeur_gauche,arbre_gauche_gauche,arbre_gauche_droite),(valeur_droite,arbre_droite_gauche,arbre_droite_droite)), mais comme « arbre_gauche_gauche » sera lui-même représenté par un tuple… Nous allons donc avoir des tuples qui contiendront des tuples qui eux-mêmes contiendront des tuples…
Pour l’arbre binaire défini ci-dessus, on aura :
('A', ('B', ('C', None, ('E', None, None)), ('D', None, None)), ('F', ('G', ('I', None, None), None), ('H', None, ('J', None, None))))
Voici le programme augmenté de la fonction « affiche » :
class ArbreBinaire:
def __init__(self, valeur):
self.valeur = valeur
self.enfant_gauche = None
self.enfant_droit = None
def insert_gauche(self, valeur):
if self.enfant_gauche == None:
self.enfant_gauche = ArbreBinaire(valeur)
else:
new_node = ArbreBinaire(valeur)
new_node.enfant_gauche = self.enfant_gauche
self.enfant_gauche = new_node
def insert_droit(self, valeur):
if self.enfant_droit == None:
self.enfant_droit = ArbreBinaire(valeur)
else:
new_node = ArbreBinaire(valeur)
new_node.enfant_droit = self.enfant_droit
self.enfant_droit = new_node
def get_valeur(self):
return self.valeur
def get_gauche(self):
return self.enfant_gauche
def get_droit(self):
return self.enfant_droit
#######fin de la classe########
######début de la construction de l'arbre binaire###########
racine = ArbreBinaire('A')
racine.insert_gauche('B')
racine.insert_droit('F')
b_node = racine.get_gauche()
b_node.insert_gauche('C')
b_node.insert_droit('D')
f_node = racine.get_droit()
f_node.insert_gauche('G')
f_node.insert_droit('H')
c_node = b_node.get_gauche()
c_node.insert_droit('E')
g_node = f_node.get_gauche()
g_node.insert_gauche('I')
h_node = f_node.get_droit()
h_node.insert_droit('J')
######fin de la construction de l'arbre binaire###########
def affiche(T):
if T != None:
return (T.get_valeur(),affiche(T.get_gauche()),affiche(T.get_droit()))
À faire vous-même 3
Vérifiez que « affiche(racine) » renvoie bien :
('A', ('B', ('C', None, ('E', None, None)), ('D', None, None)), ('F', ('G', ('I', None, None), None), ('H', None, ('J', None, None))))
N.B : la fonction « affiche » n’a pas une importance fondamentale, elle sert uniquement à vérifier que les arbres programmés sont bien corrects.
À faire vous-même 4
Programmez à l’aide de la classe « ArbreBinaire », l’arbre binaire suivant :
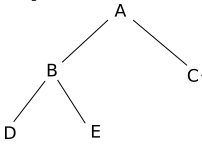
Arbre 2
Vérifiez votre programme à l’aide de la fonction « affiche »
Vous allez maintenant pouvoir commencer à travailler sur l’implémentation des algorithmes sur les arbres binaires :
À faire vous-même 5
Programmez la fonction « hauteur » qui prend un arbre binaire T en paramètre et renvoie la hauteur de T (algorithme correspondant, voir ici)
Testez votre fonction en utilisant l’arbre vu plus haut (schéma « Arbre 1 »).
À faire vous-même 6
Programmez la fonction « taille » qui prend un arbre binaire T en paramètre et renvoie la taille de T (algorithme correspondant, voir ici)
Testez votre fonction en utilisant l’arbre vu plus haut (schéma « Arbre 1 »).
À faire vous-même 7
Programmez la fonction « parcours_infixe » qui prend un arbre binaire T en paramètre et qui permet d’obtenir le parcours infixe de l’arbre T (algorithme correspondant, voir ici)
Testez votre fonction en utilisant l’arbre vu plus haut (schéma « Arbre 1 »).
À faire vous-même 8
Programmez la fonction « parcours_prefixe » qui prend un arbre binaire T en paramètre et qui permet d’obtenir le parcours préfixe de l’arbre T (algorithme correspondant, voir ici)
Testez votre fonction en utilisant l’arbre vu plus haut (schéma « Arbre 1 »).
À faire vous-même 9
Programmez la fonction « parcours_suffixe » qui prend un arbre binaire T en paramètre et qui permet d’obtenir le parcours suffixe de l’arbre T (algorithme correspondant, voir ici)
Testez votre fonction en utilisant l’arbre vu plus haut (schéma « Arbre 1 »).
À faire vous-même 10
Programmez la fonction « parcours_largeur » qui prend un arbre binaire T en paramètre et qui permet d’obtenir le parcours en largeur de l’arbre T (algorithme correspondant, voir ici)
Testez votre fonction en utilisant l’arbre vu plus haut (schéma « Arbre 1 »).
Nous allons maintenant travailler sur les arbres binaires de recherche.
À faire vous-même 11
Programmez, à l’aide de la classe « ArbreBinaire », l’arbre binaire de recherche ci-dessous : 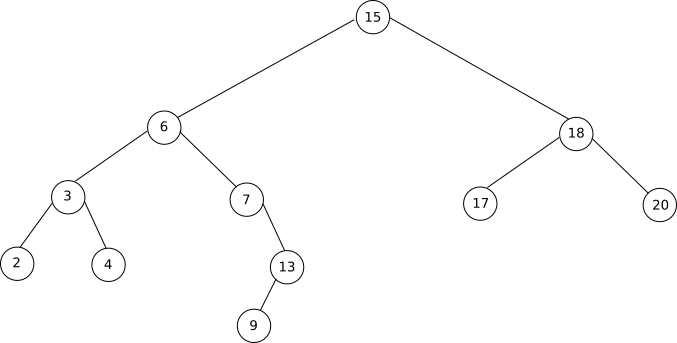 Arbre 3
Arbre 3
Vérifiez votre réponse à l’aide de la fonction « affichage »
À faire vous-même 12
Afin de vérifier que l’arbre binaire « Arbre 3 » est bien un arbre binaire de recherche, utilisez la fonction « parcours_infixe » programmée dans le « À faire vous-même 7 ».
À faire vous-même 13
Programmez la fonction « arbre_recherche » qui prend un arbre binaire T et un entier k en paramètres et qui renvoie True si k appartient à T et False dans le cas contraire (algorithme correspondant, voir ici)
Testez votre fonction en utilisant l’arbre vu plus haut (schéma « Arbre 3 ») avec k = 13 et k = 16.
À faire vous-même 14
Programmez la fonction « arbre_recherche_ite » (version itérative de la fonction « arbre_recherche ») qui prend un arbre binaire T et un entier k en paramètres et qui renvoie True si k appartient à T et False dans le cas contraire (algorithme correspondant, voir ici)
Testez votre fonction en utilisant l’arbre vu plus haut (schéma « Arbre 3 ») avec k = 13 et k = 16.
À faire vous-même 15
Programmez la fonction « arbre_insertion » qui prend T (un arbre binaire) et y (un objet de type « ArbreBinaire ») en paramètres et qui insert y dans T (algorithme correspondant, voir ici)
Testez votre fonction en utilisant l’arbre vu plus haut (schéma « Arbre 3 ») avec y.valeur = 16.

Auteur : David Roche