NSI Première
NSI Terminale
Archives de catégorie : NSI
Tri par insertion
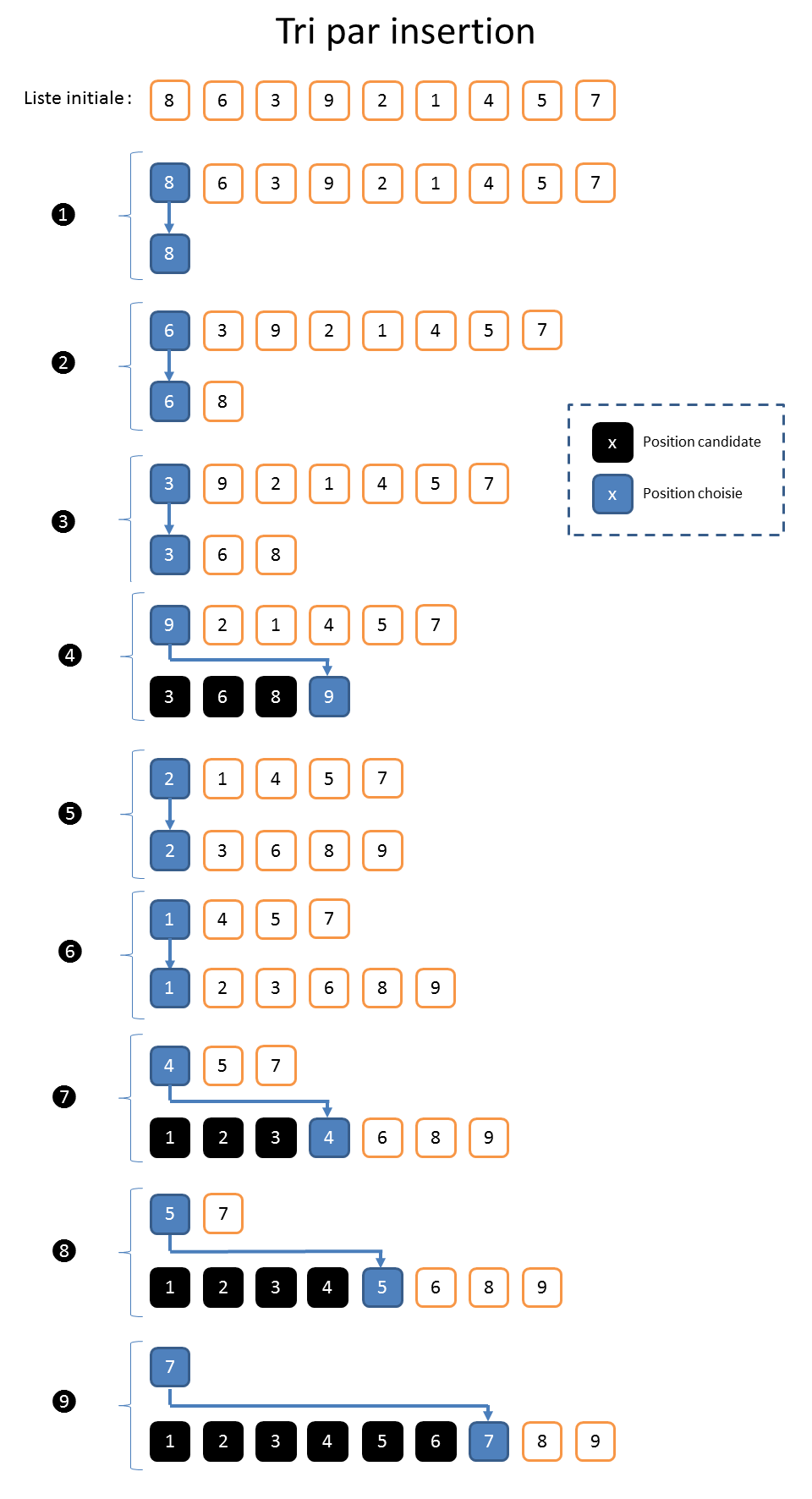
Vous avez certainement utilisé cet algorithme, C’est celui que les joueurs de cartes utilisent pour organiser leurs mains. Le joueur pioche la carte qui est en haut du tas et la place (l’insère) à la bonne position dans la main. Cet algorithme se nomme le « tri par insertion ».
Pour simplifier nous allons trier une liste de 9 valeurs
[ 8, 6, 3, 9, 2, 1, 4, 5, 7 ]
pour commencer l’explication , utilisons 2 listes
A faire:
Réaliser le même schéma avec [ 5, 12, 3, 7, 4 ] sur le document Libre Office réponse joint.
Combien de comparaison? pour trier [ 8, 6, 3, 9, 2, 1, 4, 5, 7 ]
La première valeur pas de comparaison, on la prend et la pose en premier, la deuxième valeur à classer je la compare à la première ordonnée et je la pose devant ou derrière. Pour la troisième valeur , deux comparaison et ainsi de suite jusqu’à la dernière huit comparaison donc nous avons fait 1+2+3+4+5+6+7+8 comparaison soit 36 comparaison.
A faire: à vous par extension pour une liste à n éléments:
Voici une implémentation sous python avec 2 tableaux ou listes comme le graphique ci dessus
def tri_insertion(tableau):
'''cette fonction prend en argument un tableau (tableau), et le trie avec la méthode de tri par insertion, elle renvoie le tableau trié (resultat)
exemple:
tri_insertion([22,8,32,1,69])
>>> [1,8,22,32,69]
tri_insertion([18,41,7,2,14])
>>> [2,7,14,18,41]'''
resultat=[]
longueur = len(tableau)
while len(resultat) < longueur:
'''tant que la taille du résultat n'est pas le même que celui du tableau initial'''
for indice in range(0,longueur):
compteur = 0
placer = True
if resultat == []:
resultat.append(tableau[0])
del tableau[0]
for valeur_resultat in resultat:
if tableau == []:
return resultat
if valeur_resultat < tableau[0]:
compteur += 1
elif placer:
placer = False
resultat.insert(compteur, tableau[0])
del tableau[0]
compteur = 0
if placer:
resultat.append(tableau[0])
del tableau[0] voici l’algorithme du tri par insertion ( ici une seule liste )
- PROCEDURE tri_Insertion ( Tableau a[1:n])
- POUR i VARIANT DE 2 A n FAIRE
- INSERER a[i] à sa place dans a[1:i-1];
- FIN PROCEDURE;
en python à essayer
def tri_insertion(tableau):
print(tab)#affiche la liste tab pour visualiser l'algo
for i in range(1,len(tableau)):
en_cours = tableau[i]
j = i
#décalage des éléments du tableau }
while j>0 and tableau[j-1]>en_cours:
tableau[j]=tableau[j-1]
j = j-1
#on insère l'élément à sa place
tableau[j]=en_coursvous pouvez trouver des explications supplémentaire ici:
site de podcastscience , site de David Roche et sur le site http://lwh.free.fr
Retour vers article algorithme de tri
Tri par sélection
Pour simplifier nous allons trier une liste de 9 valeurs
[ 8, 6, 3, 9, 2, 1, 4, 5, 7 ]
pour commencer l’explication , utilisons 2 listes
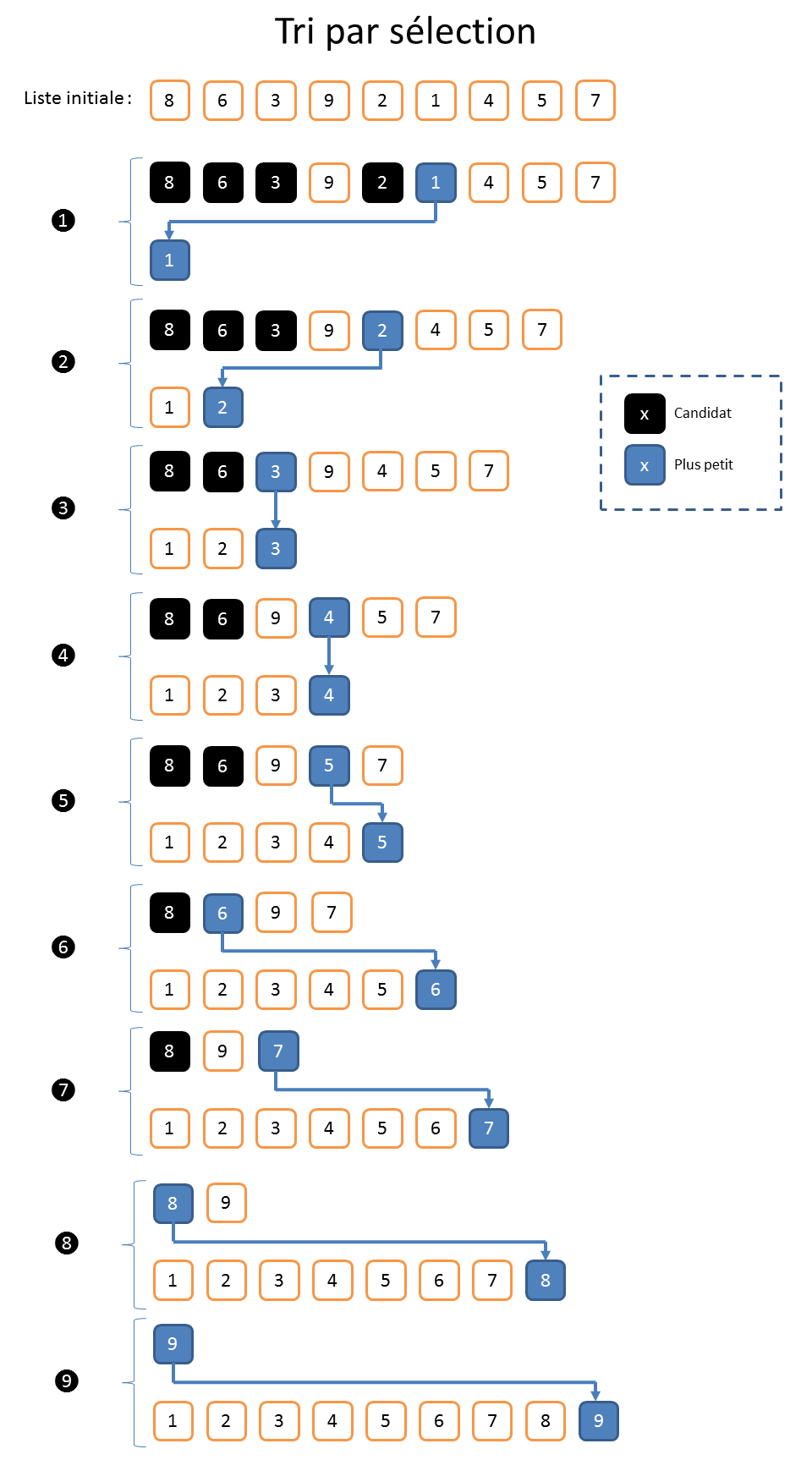
A faire: sur le document réponse Libre Office.
Réaliser le même schéma avec [ 5, 12, 3, 7, 4 ] sur le document réponse Libre Office. En fin de document vous pouvez découper les numéros pour faire une simulation à la main.
Combien de comparaison? pour trier [ 8, 6, 3, 9, 2, 1, 4, 5, 7 ]
pour sélectionner l’élément le plus petit on liste les 9 valeurs et on fait 8 comparaisons, pour le deuxième on fait 7 comparaisons, pour le troisième 6 comparaisons et ainsi de suite. D’où nombre de comparaison= 8+7+6+….+1=36.
Par extension si notre liste est constituée de n valeurs, le nombre de comparaison = (n-1)+(n-2)+(n-3)+ …..+3+2+1 en factorisant nombre de comparaison=n*(n-1) /2 soit n²/2-n/2 .
On dit que l’algorithme de tri par sélection a donc une complexité en O(n²). On parle aussi de complexité quadratique.
Voici une implémentation sous python avec 2 tableaux ou listes comme le graphique ci dessus
def tri_selection(tableau):
'''tri d'un tableau, l'argument tableau est un tableau ou liste, la fonction renvoie un autre tableau ou liste resultat'''
resultat = []
longueur = len(tableau)
while len(resultat) != longueur:
minimum = tableau[0]
for i in range(1, len(tableau)):
if minimum > tableau[i]:
minimum = tableau[i]
resultat.append(minimum)
tableau.remove(minimum)
return resultat voici l’algorithme du tri par sélection ( ici une seule liste )
- PROCEDURE tri_Selection ( Tableau a[1:n])
- POUR i VARIANT DE 1 A (n – 1) FAIRE
- TROUVER [j] LE PLUS PETIT ELEMENT DE [i + 1:n];
- ECHANGER [j] ET [i];
- FIN PROCEDURE;
en python à essayer
def tri_selection(tab):
print(tab)
for i in range(len(tab)):#boucle sur toute la liste
# Trouver le min
min = i
for j in range(i+1, len(tab)):
if tab[min] > tab[j]:
min = j
tmp = tab[i]
print('tmp',tmp)#affiche tmp pour visualiser l'algo
tab[i] = tab[min]
print ('tab1',tab)#affiche la liste tab pour visualiser l'algo
tab[min] = tmp
print('tab2',tab)#affiche la liste tab pour visualiser l'algo
return tab
# Programme principale pour tester le code ci-dessus
tab = [98, 22, 15, 32, 2, 74, 63, 70]#changer les valeurs de la liste pour un autre essai
tri_selection(tab)
print ("Le tableau trié est:")
print (tab)vous pouvez trouver des explications supplémentaire ici:
site de podcastscience , site de David Roche et sur le site http://lwh.free.fr
Retour vers article algorithme de tri
Algorithmes de tri
Référence au programme de NSI
On veut trier une liste lorsqu’on pense que ses éléments sont dans le désordre, ou plus précisément dans un ordre qui ne nous convient pas. L’objectif du tri, en tant qu’algorithme, est de mettre les éléments dans le bon ordre. Par exemple sur STRAVA qui est un site et une application mobile pour enregistrer les activités sportives, l’utilisateur peut classer ses activités par années, semaines, distances parcourues, temps sur certains parcours mythiques (segment) .
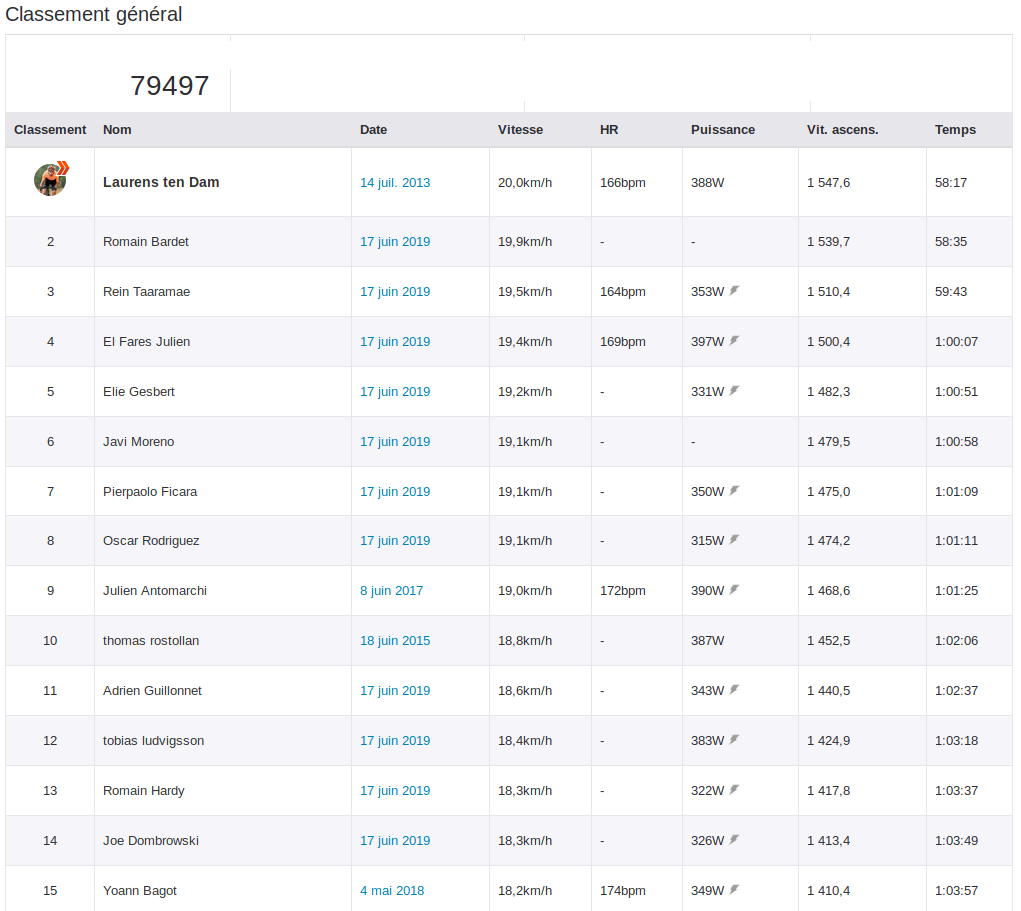
Sur ce tableau le classement est réalisé sur le temps d’ascension, par ordre croissant.
Nous allons étudier 2 algorithmes de tri :
(cliquez pour ouvrir les articles)
le tri par sélection et le tri par insertion.
Nous avons calculer le nombre comparaison que faisait les algorithmes dans le tri par insertion et sélection, On parle de complexité . La complexité d’un tri de « n » éléments se note avec un « omicron » : dites « grand O ». Par exemple, la complexité du « tri par sélection » sera en « O(n*(n-1) /2 ) », où « n*(n-1) /2 » est la formule qu’on avait utilisée un peu plus tôt. Comme on s’intéresse à des valeurs importantes et qu’on ne veut qu’un « ordre de grandeur », on considérera que cette « complexité » peut se « simplifier » en « O(n*(n-1)) », qui peut elle-même se simplifier en « O(n²) ». On dira que l’algorithme du « tri par sélection » est de « complexité quadratique » en « O(n²) ».
Pour notre classement il y a 80 000 valeurs à trier voici un tableau résumant le nombre d’opération et une estimation du temps en supposant qu’une opération dure 1 ms.
| Nombre d’éléments « n » | Nombre d’opérations pour un tri en « O(n²) » | Durée pour un tri en « O(n²) » |
| 10 | 100 | 100 ns |
| 100 | 10 000 | 10 us |
| 1 000 | 1 000 000 | 1 ms |
| 10 000 | 100 000 000 | 100 ms |
| 100 000 | 10 000 000 000 | 10 s |
| 1 000 000 | 1 000 000 000 000 | 16 min 40 s |
| 10 000 000 | 100 000 000 000 000 | 27 heures |
| 100 000 000 | 10 000 000 000 000 000 | 115 jours |
| 1 000 000 000 | 1 000 000 000 000 000 000 | 31 ans |
Il y a 1.2 millions d’utilisateur de Strava , 3.4 milliard d’utilisateur de Facebook . Les données à trier ne manquent pas….Et le temps de les trier elles seront peut être obsolètes.
Comment faire ? Il existe des algorithmes de tri plus performant: Tri à bulles , Tri rapide , ….
A faire:
Essai évaluation par le temps d’exécution du programme de tri:
Estimation de complexité par le temps d’exécution (approximation car le temps d’exécution d’un algorithme est aussi lié à d’autres paramètres… )
En ouvrant et exécutant le programme de tri :
tris-avec_evaluation-temps-execution_programme.py
à télécharger en fin d’article.
extrait du programme
# tri rapide avec affichage du temps passé
debut_chrono=time.time() # lancement chrono
trirapide(L) # lancement du tri
temps_exe=time.time()-debut_chrono #arret chrono et calcul du temps
print("nombre de valeur =",len(L)) # affichage nb valeurs
print("temps execution tri rapide =",temps_exe) # affichage crhono
Essayer de lancer ce programme en testant une liste aléatoire de 10, 100 , 1000, 10000 valeurs, faire un classement des tris.
Maintenant au lieu de trier une liste aléatoire, trions une liste déjà triée. Refaites votre classement .
Quelles conclusions tirez vous de vouloir classer la complexité d’un algorithme par son temps d’exécution?
(Rappel les deux algorithme fusion et insertion ont la même complexité)
Mini projet:
Amélioration , Il vaudrait mieux compter le nombre d’opération de comparaison dans l’algorithme de tri. Proposer une solution de compteur dans le programme de tri de votre choix
vous trouverez ici tous les fichiers à télécharger.