Présentation du projet :
Vous allez travailler sur le jeu de données suivant (à télécharger):
Ce jeu de données contient des informations sur une partie des passagers (plus exactement sur 891 passagers) du Titanic. Pour un petit rappel historique, vous pouvez consulter la page Wikipédia consacrée à ce paquebot : ici
Ouvrez le fichier « titanic.csv » à l’aide d’un tableur.
Vous devriez obtenir quelque chose qui ressemble à ceci :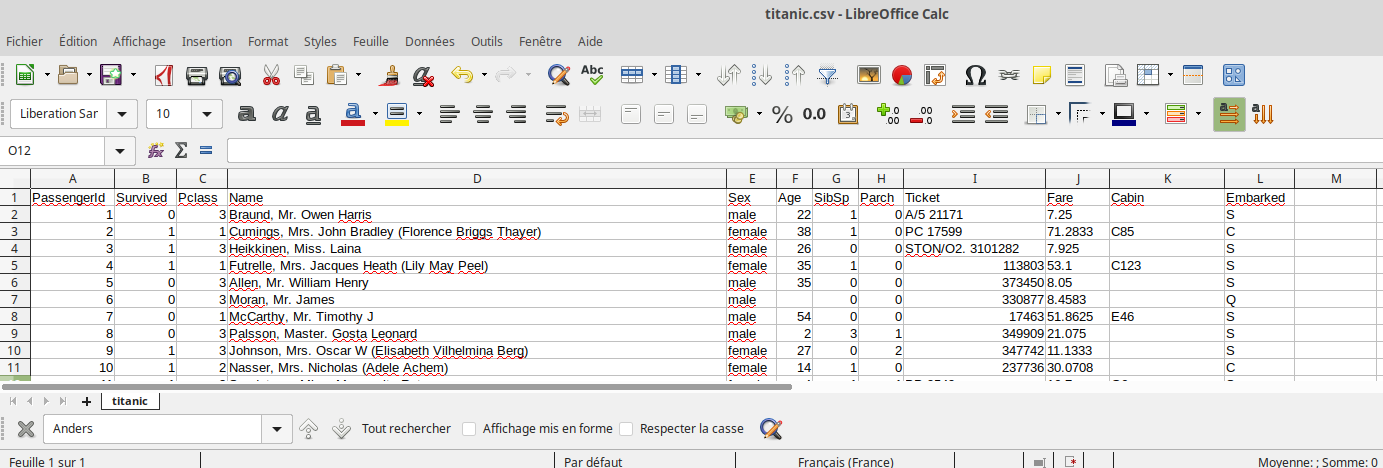
Trouvez la signification des différents descripteurs : « PassengerId », « Survived », « Pclass »… Aide :
L’objectif de ce projet est d’utiliser l’algorithme des k plus proches voisins afin de déterminer si les passagers ci-dessous auraient survécus au naufrage du Titanic.
| Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Embarked |
|---|---|---|---|---|---|---|---|---|
| 2 | Mr. Bidochon Robert | male | 37 | 1 | 4 | 244377 | 21.075 | C |
| 2 | Mrs. Bidochon Raymonde | female | 36 | 1 | 4 | 244379 | 20.2175 | C |
| 2 | Mrs. Bidochon Gisèle | female | 11 | 3 | 2 | 244382 | 15.045 | C |
| 2 | Mr. Bidochon René. | male | 8 | 3 | 2 | 244383 | 12.945 | C |
| 2 | Mr. Bidochon Eugène. | male | 4 | 3 | 2 | 137383 | 10.17 | C |
| 2 | Mr. Bidochon Louis. | male | 1 | 3 | 2 | 3738 | 11.13 | C |
PARTIE 1 : Analyse des données (Data scientist)
Un travail de préparation des données va être nécessaire , vous allez donc devoir passer par quelques étapes que voici :
– Pour ceux qui ne souhaitent pas poursuivre la spécialité N.S.I vous pouvez opérer les changements directement avec le tableur.
– Pour ceux qui souhaitent poursuivre la spécialité N.S.I vous devez opérer les changements directement avec python.
Le fichier python ci-dessous, vous aidera faire les manipulations nécessaires).
Analyser ce fichier, combien y a t’il de fonctions,que font elles?
Pour la suite du projet vous pouvez travailler soit avec la liste de dictionnaire créé avec le programme, soit avec le fichier csv.
Toutes les colonnes ne vont pas forcement être pertinentes, par exemple, d’après vous, lors du naufrage, le nom du passager a-t-il eu une quelconque importance sur le fait qu’il ait ou non survécu ? (nous ne tiendrons pas compte du fait que certaines personnes aient pu être privilégié au vu de leur nom de famille, sur les 891 passagers présents dans le fichier titanic.csv, ce phénomène est négligeable).
Solution 1 avec le tableur:
En analysant le contenu du fichier titanic.csv (par exemple à l’aide d’un tableur), choisissez les descripteurs ( c’est à dire les colonnes) qui vous paraissent les plus pertinents. Vous effacerez les colonnes qui vous semblent inutiles directement dans le tableur ou avec python pour obtenir soit une liste de dictionnaire (comme Data dans le fichier donné ci dessus), soit un nouveau fichier titanic_V2.csv
Solution 2, avec python :
Nettoyer la liste de dictionnaire, en ne gardant pour chaque dictionnaire que les clés que vous jugez nécessaire.
Enregistrer votre fichier python.
Pour certains passagers, il manque des données. Par exemple, l’âge de certains passagers n’est pas renseigné. Une solution est de supprimer du fichier les passagers ayant des données incomplètes.
Supprimer du fichier les passagers ayant des données incomplètes pour obtenir un nouveau fichier titanic_V3.csv ou une nouvelle liste de dictionnaire avec les données incomplètes supprimées.
L’utilisation de l’algorithme des k plus proches voisins nous oblige à proscrire les données non numériques.
Par exemple, la colonne « Sex » ne peut pas être utilisée telle quelle, l’algorithme n’est pas capable de traiter les « male » et « female ».
Proposer une alternative pour remplacer les chaines de caracteres « male » et « female ».
Modifier certaines colonnes directement dans le tableur ou avec un script python pour obtenir un nouveau fichier titanic_V4.csv ou une nouvelle liste de dictionnaire.
Avec l’algorithme des k plus proches voisins nous sommes amenés à calculer des distances.
Comparer l’amplitude des valeurs de la colonne Pclass avec l’amplitude des valeurs de la colonne Age.
Amplitude des valeurs de la colonne Pclass :
Amplitude des valeurs de la colonne Age :
Code python pour obtenir cette amplitude à partir de titanic_V4.csv ou avec la liste de dictionnaire :
Une des conséquence de l’observation précédente est que le calcul de la distance ne va pas traiter de facon égalitaire les colonnes.
Pour rétablir l’équité nous allons procéder ainsi :
Pour chaque colonne :
- On repère la valeur minimale (v_min) et la valeur maximale ( v_max)
- On va diviser chacune des valeurs de la colonne par la diffrence v_max-v_min
Exemple : Si une colonne contient les valeurs [5,4,1,11,7]
v_min=1 et v_max=11
Alors on divise toutes les valeurs par 8 ce qui donne [0.5,0.4,0.1,1.1,0.7]
Remarque :
Toutes les valeurs de toutes les colonnes seront comprises entre 0 et 1.
Cela nous garantie un traitement équitable entre les colonnes.
Faire les modifications nécessaires au fichier titanic_V4.csv pour garantir un équitable entre les colonnes. On nommera titanic_V5.csv le nouveau fichier obtenu. Vous devriez avoir un fichier comme celui-ci:
Partie 2: Graphique 3D
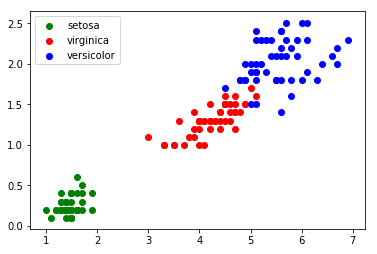
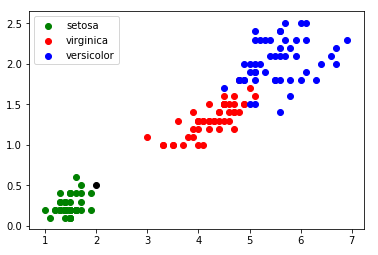
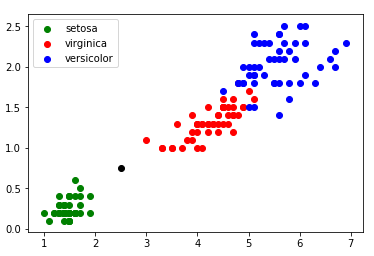
A l’aide du TP sur les k plus proches voisins, construire le graphique 3D à partir du fichier titanicV5.csv
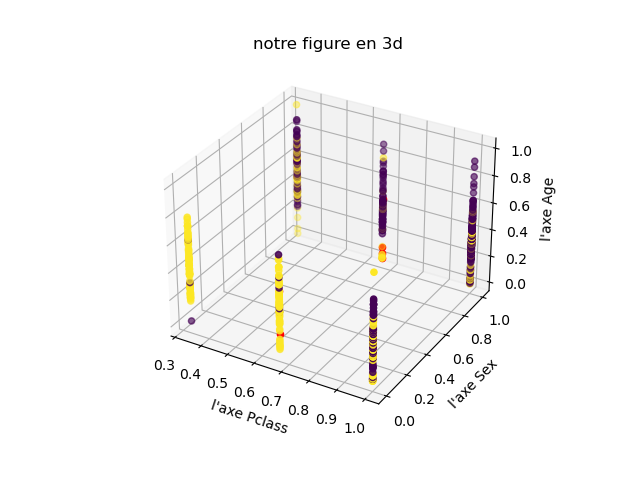
Les survivants devront être en vert et les disparus en rouge, les personnes que vous testerez seront en bleu.
voici quelques liens ou faire des recherches:
1 er lien Les fiches CPGE
2 éme lien Machine learnia
Partie 3: Utilisation de l’algorithme des K plus proche voisins
A l’aide du TP sur les k plus proches voisins, (avec k=5) prédire quel(s) membre(s) de la famille Bidochons aurait(ent) survécu(s) au naufrage du Titanic ?
En utilisant l’algorithme proposé par scikit-learn
des k plus proches voisins établir votre programme python et donnez la liste des survivants en faisant varier k de 3 à 19 ( valeur impaire).
( c’est la ligne : from sklearn.neighbors import KNeighborsClassifier qui charge l’algorithme)