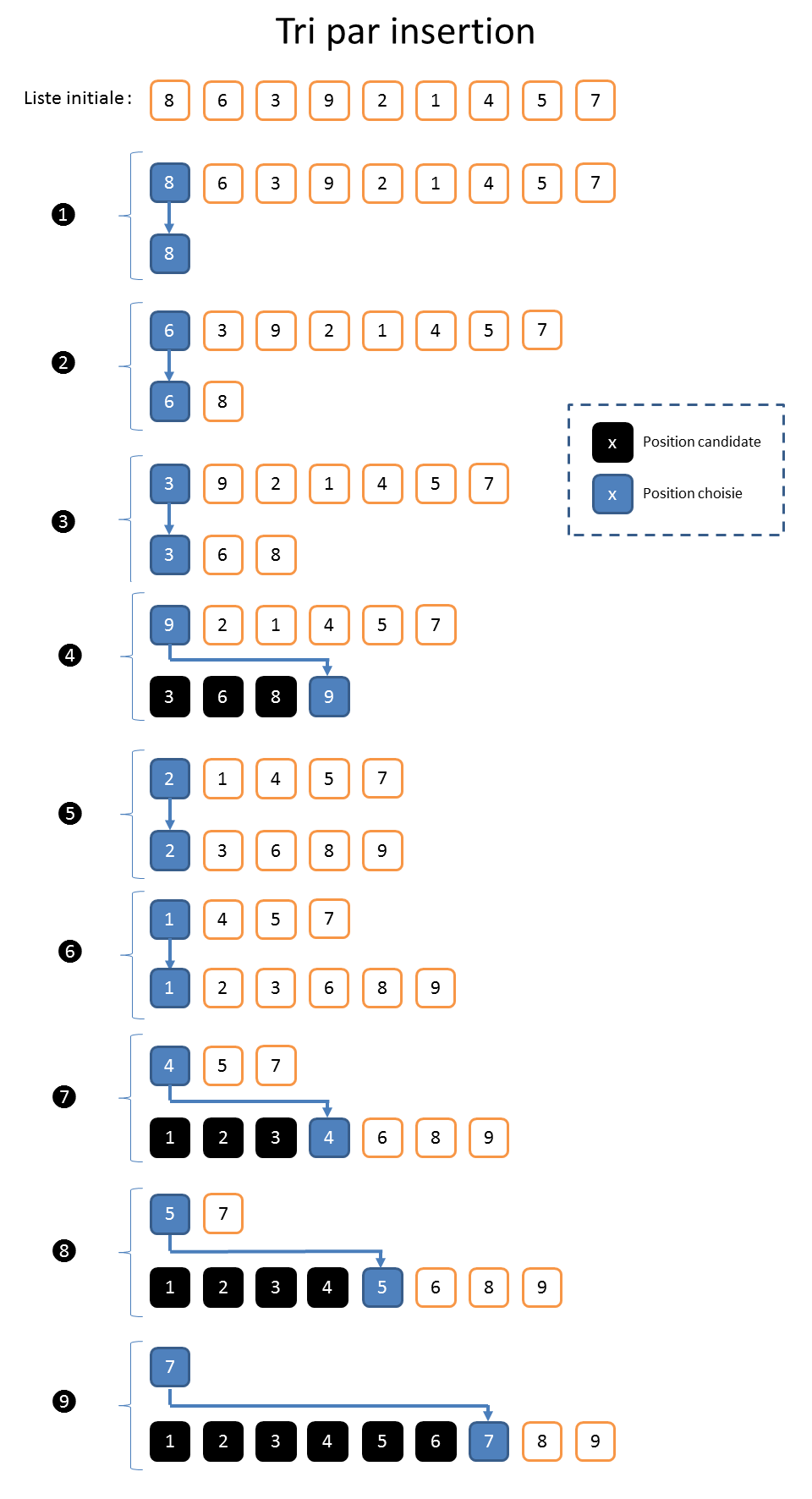
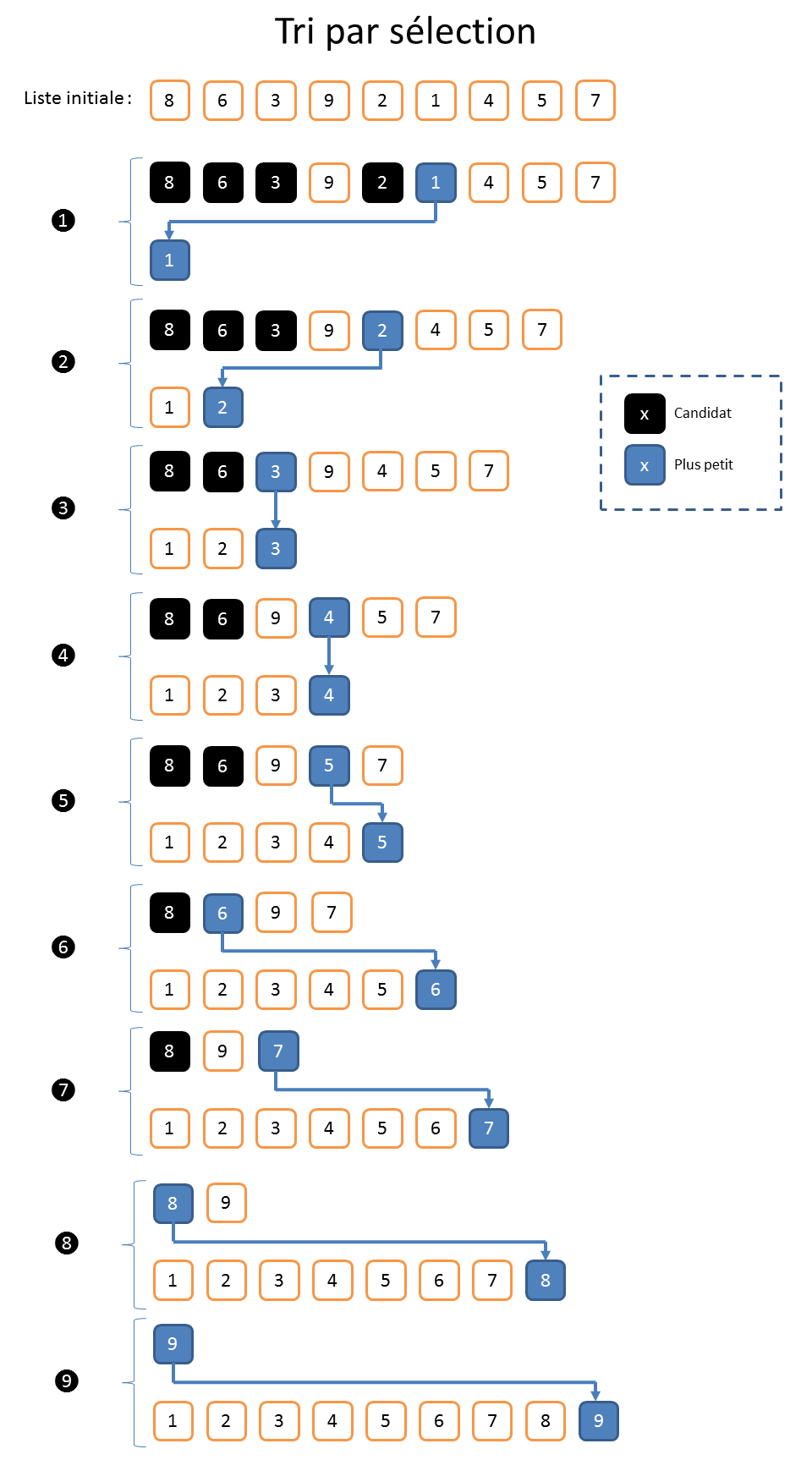
5.1. Pourquoi a-t-on besoin de fonctions ?
Étudions le programme ci-dessous qui calcule et affiche la moyenne de 4 élèves sur trois notes: (Exécuter le programme ci-dessous)
prenom1 = "Anne"
note1 = 13
note2 = 10
note3 = 16
moyenneA = (note1 + note2 + note3) / 3
print("La moyenne de ", prenom1, " est : ", moyenneA)
prenom2 = "Boris"
note4 = 9
note5 = 7.5
note6 = 12
moyenneB = (note4 + note5 + note6) / 3
print("La moyenne de ", prenom2, " est : ", moyenneB)
prenom3 = "Céline"
note7 = 8
note8 = 12
note9 = 16
moyenneC=(note7 + note8 + note9) / 3
print("La moyenne de ", prenom3, " est : ", moyenneC)
prenom4 = "Denis"
note10 = 11
note11 = 14
note12 = 17
moyenneD = (note10 + note11 + note12) / 3
print("La moyenne de ", prenom4, " est : ", moyenneD)Que se passe-t il si on ajoute 2 nouveaux élèves dans le groupe ? On ré-écrit le code de calcul de la moyenne pour les notes de ces élèves là. Un peu ennuyant.
Que se passe-t-il si on veux ajouter une note supplémentaire ?
prenom1 = "Anne"
note1 = 13
note2 = 10
note3 = 16
note_sup = 14
moyenneA=(note1 + note2 + note3 + note_sup) / 4
print("La moyenne de ", prenom1, " est : ", moyenneA)On doit ajouter une note pour Anne, et on change le calcul de la moyenne en ajoutant la note supplémentaire et en divisant par 4. Et ensuite, on doit faire cela pour Boris, Celine, Denis et les deux nouveaux… Fastidieux !
Que se passe-t-il si on veut en plus afficher un message selon la moyenne obtenue?
Exemple pour Anne et Boris:
prenom1="Anne"
note1=13
note2=10
note3=16
note_sup=14
moyenneA=(note1+note2+note3+note_sup)/4
print("La moyenne de ", prenom1, " est : ",moyenneA)
if moyenneA>11:
print("C'est en bonne voie")
else:
print("Persévérez !")
prenom2="Boris"
note4=9
note5=7.5
note6=12
note_sup2=8
moyenneB=(note4+note5+note6+note_sup2)/4
print("La moyenne de ", prenom2, " est : ",moyenneB)
if moyenneB>11:
print("C'est en bonne voie")
else:
print("Persévérez !")On a joute du code pour chaque élève qui se ressemble. Ça commence à devenir long, compliqué, et on peut facilement se tromper, alors que les tâches sont très répétitives !
Quand une tâche peut être effectuée plusieurs fois dans un programme, il devient vite TRÈS INTÉRESSANT d’utiliser un morceau de programme qu’on va réutiliser : on isole alors ce morceau de code dans un BLOC qu’on appelle FONCTION
Exemple (la syntaxe de la fonction sera expliquée plus loin) :
#bloc fonction qui calcule et affiche la moyenne
def calcule_et_affiche_moyenne(prenom,note1,note2,note3):
moyenne=(note1+note2+note3)/3
print("La moyenne de ", prenom, " est : ",moyenne)
#appels répétés de la fonction dans le programme principal
calcule_et_affiche_moyenne("Anne", 13,10,16)
calcule_et_affiche_moyenne("Boris", 9,7.5,12)
calcule_et_affiche_moyenne("Céline", 8,12,16)
calcule_et_affiche_moyenne("Denis", 11,14,17)Ce qu’on a gagné :
On a écrit une seule fois le calcul de la moyenne. Si on ajoute 2 élèves, on appelle 2 fois la fonction Si on ajoute une note, on ne change que le contenu de la fonction calcule_et_affiche_moyenne() Si on veut ajouter l’affichage d’un message, on peut le faire dans la fonction sans changer le programme principal
Par exemple :
#bloc qui affiche un message d'encouragement
def affiche_message(moyenne):
if moyenne>11:
print("C'est en bonne voie")
else:
print("Persévérez !")
#bloc fonction qui calcule et affiche la moyenne
def calcule_et_affiche_moyenne(prenom,note1,note2,note3):
moyenne=(note1+note2+note3)/3
print("La moyenne de ", prenom, " est : ",moyenne)
affiche_message(moyenne)
#appels répétés de la fonction dans le programme principal
calcule_et_affiche_moyenne("Anne", 13,10,16)
calcule_et_affiche_moyenne("Boris", 9,7.5,12)
calcule_et_affiche_moyenne("Céline", 8,12,16)
calcule_et_affiche_moyenne("Denis", 11,14,17)
Comparez maintenant ce dernier programme avec le premier : avec moins de lignes de programme, on fait plus de choses, et en plus ça reste très lisible ! c’est aussi très utile si la personne qui définit la fonction est différente de celle qui l’utilise on peut ainsi utiliser une fonction que l’on n’a pas codé sois même, simplement, on l’appelle ! Comme par exemple la fonction print()
Un script bien structuré contiendra un programme dit principal, et plusieurs sous-programmes codés dans des fonctions dédiées à des fonctionnalités spécifiques.

5.2. Syntaxe : comment écrire une fonction
La syntaxe Python pour la définition d’une fonction est la suivante :
def nom_fonction(liste de paramètres):
bloc d'instructions #corps de la fonctionVous pouvez choisir le nom de votre choix pour la fonction que vous créez, sauf les mots-clés réservés du langage (par exemple if, while…), sans utiliser de caractère spécial ou accentué (le caractère souligné « _ » est autorisé).
On utilise par convention des minuscules, notamment au début du nom.
Comme les instructions if, for et while l’instruction def est une instruction composée. La ligne contenant cette instruction se termine obligatoirement par un deux-points :, qui introduisent un bloc d’instructions qui est précisé grâce à l’indentation. Ce bloc d’instructions constitue le corps de la fonction.
def calcule_somme(note1,note2,note3):
somme = (note1+note2+note3) # corps de
return somme # la fonction
print(calcule_somme(128,1256,322))5.3. Fonctions et paramètres
Fonction sans paramètre.
Exemple :
def bonjour():
print("Bonjour")
def compteur():
for i in range(3):
print(i)
Nous avons défini une première fonction qui affiche le texte Bonjour et une deuxième fonction simple qui affiche les entier de 0 à 4.
Notez bien les parenthèses, les deux-points, et l’indentation du bloc d’instructions qui suit la ligne d’en-tête (c’est ce bloc d’instructions qui constitue le corps de la fonction proprement dite).
Avoir une fonction, c’est bien mais encore faut-il l’utiliser :
bonjour()
compteur()
Nous pouvons maintenant réutiliser cette fonction à plusieurs reprises, autant de fois que nous le souhaitons.
Nous pouvons également l’incorporer dans la définition d’une autre fonction.
Exemple de fonction qui appelle une autre fonction :
def poli():
for i in range(3):
bonjour()
poli()
Une première fonction peut donc appeler une deuxième fonction, qui elle-même en appelle une troisième, etc.
Créer une nouvelle fonction offre l’opportunité de donner un nom à tout un ensemble d’instructions. De cette manière, on peut simplifier le corps principal d’un programme, en dissimulant un algorithme secondaire complexe sous une commande unique, à laquelle on peut donner un nom explicite.
Une fonction est donc en quelque sorte une nouvelle instruction personnalisée, qu’il est possible d’ajouter librement à notre langage de programmation.
Fonction avec paramètres.
Exemple :
def bonjour(nom):
print("Bonjour {}".format(nom))
def compteur(stop):
for i in range(stop):
print(i)
compteur(5)
Pour tester ces fonctions, il faut les appeler avec un argument :
bonjour("toto")
compteur(4)
On peut bien sûr avoir des fonctions qui appellent des fonctions :
def trespoli(nbfois):
for i in range(nbfois):
bonjour("tata toto")
trespoli(3)
Utilisation d’une variable comme argument.
L’argument que nous utilisons dans l’appel d’une fonction peut être une variable.
Exemple :
a = "Bart Simpson" bonjour(a)
Dans l’exemple ci-dessus, l’argument que nous passons à la fonction bonjour() est le contenu de la variable a.
À l’intérieur de la fonction, cet argument est affecté au paramètre stop, qui est une tout autre variable.
Notez donc bien dès à présent que :
- Le nom d’une variable que nous passons comme argument n’a rien à voir avec le nom du paramètre correspondant dans la fonction.
- Ces noms peuvent être identiques si vous le voulez, mais vous devez bien comprendre qu’ils ne désignent pas la même chose (en dépit du fait qu’ils puissent contenir une valeur identique).
Fonction avec plusieurs paramètres.
Exemples :
def bonjour(prenom, nom):
print("Bonjour " + prenom + " " + nom)
bonjour("Homer","Simpson")
bonjour("Marge","Simpson")
La fonction suivante utilise trois paramètres : start qui contient la valeur de départ, stop la borne supérieure exclue comme dans l’exemple précédent et step le pas du compteur :
def compteur(start, stop, step):
for i in range(start, stop, step):
print(i)
compteur(1, 7, 2)
À retenir:
- Pour définir une fonction avec plusieurs paramètres, il suffit d’inclure les paramètres entre les parenthèses qui suivent le nom de la fonction, en les séparant à l’aide de virgules.
- Lors de l’appel de la fonction, les arguments utilisés doivent être fournis dans le même ordre que celui des paramètres correspondants (en les séparant eux aussi à l’aide de virgules).
Le premier argument sera affecté au premier paramètre, le second argument sera affecté au second paramètre, et ainsi de suite.
def politesse(nom, titre ="Monsieur"):
print("Veuillez agréer,", titre, nom, ", mes salutations distinguées.")
politesse("Dupont")
Valeurs par défaut pour les paramètres
Dans la définition d’une fonction, il est possible de définir un argument par défaut pour chacun des paramètres. On obtient ainsi une fonction qui peut être appelée avec une partie seulement des arguments attendus.
Exemples :
def compteur(start, stop, step=1):
for i in range(start, stop, step):
print(i)
compteur(1, 4)
Lorsque l’on appelle cette fonction en ne lui fournissant que les deux premier arguments, le troisième argument step second reçoit tout de même une valeur par défaut (ici 1).
alors que l’oubli d’un paramètre amène à une erreur comme ci-dessous.
def compteur(start, stop, step):
for i in range(start, stop, step):
print(i)
compteur_complet(1, 7)
Arguments avec étiquettes
Dans la plupart des langages de programmation, les arguments que l’on fournit lors de l’appel d’une fonction doivent être fournis exactement dans le même ordre que celui des paramètres qui leur correspondent dans la définition de la fonction.
Python autorise l’appel aux fonctions en fournissant les arguments correspondants dans n’importe quel ordre, à la condition de désigner nommément les paramètres correspondants.
Exemple :
def compteur(start, stop, step):
for i in range(start, stop, step):
print(i)
compteur_complet(step=2, stop=4, start=1)
5.4. Les fonctions avec return
Vous avez vu en mathématiques les fonctions pour un x donné retournent une valeur f(x) (éventuellement).
python utilise le mot clé return
Par exemple pour la fonction f : x ⟼ 2x + 3 on utilisera la fonction :
def f(x):
return 2*x+3
print(f(0))
print(f(1))
Les fonctions permettent donc de décomposer un programme complexe en une série de sous-programmes plus simples. De plus, les fonctions sont réutilisables : si nous disposons d’une fonction capable de calculer une racine carrée, par exemple, nous pouvons l’utiliser un peu partout dans notre programme sans avoir à la réécrire à chaque fois (on parle de factorisation du code)
La notion de fonction en informatique est comparable à la notion de fonction en mathématiques.
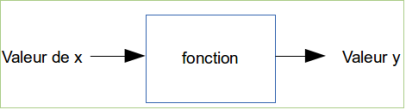
Si nous avons y = 3x+2, pour une valeur donnée de x, nous aurons une valeur de y.
Exemple : x=4 donc y= 14 (y = 3.4+2=14, attention ici le point correspond au signe « multiplié »).
La fonction en informatique est basée sur la même idée :

Voici la syntaxe employée en Python pour définir une fonction :
def nom_de_la_fonction(parametre):
instruction_1
instruction_2
return y
suite programme La fonction renvoie la valeur contenue dans la variable y.
ATTENTION : Notez bien la présence du décalage entre la première ligne et les lignes suivantes. Ce décalage est appelé indentation, l’indentation permet de définir un bloc de code. Dans l’exemple ci-dessus, l’indentation nous permet de savoir que « instruction_1« , « instruction_2 » et « return y » constituent un bloc de code, ce bloc correspond au contenu de la fonction. « suite programme » ne fait pas partie de la fonction, car il n’est pas indenté. Pour indenter du code, il y a 2 solutions : mettre 4 espaces ou utiliser une tabulation. En Python il est conseillé d’utiliser les 4 espaces, mais ce n’est pas une obligation. Une chose est sûre, une fois que vous avez choisi une méthode, n’en changez surtout pas au cours d’un même programme !
Codons notre exemple (y = 3x + 2) en créant une fonction ma_fonction :
def ma_fonction(x):
y = 3 * x + 2
return y Pour « utiliser » la fonction ma_fonction, il suffit d’écrire : ma_fonction (4) (dans ce cas précis, notre fonction renverra le nombre 14).
À faire vous-même 28
Tester le programme suivant (quelle est la valeur référencée par la variable solution après l’exécution du programme) :
def ma_fonction(x):
y = 3 * x + 2
return y
solution = ma_fonction(4) Il faut savoir qu’au moment de l’exécution de votre programme le code ma_fonction(4) sera systématiquement remplacé par la valeur renvoyée par la fonction (toujours dans notre exemple le ma_fonction(4) sera remplacé par le nombre 14).
À faire vous-même 29
Coder en Python la fonction y = x2+2x+10
Il est possible d’écrire une fonction dans l’éditeur :

et d’utiliser la console (après exécution du programme) pour obtenir la valeur renvoyée par une fonction

Il est possible de faire passer plusieurs paramètres à une fonction.
À faire vous-même 30
Quel est le résultat renvoyé par la fonction ci-dessous si l’on saisit dans la console une_autre_fonction(5, 3)
def une_autre_fonction(x, b):
y = 3 * x + b
return y Les paramètres peuvent être des chaînes de caractères (ainsi que la valeur retournée)
À faire vous-même 31
Quel est le résultat attendu après l’exécution du programme ci-dessous et la saisie dans la console de « dit_bonjour(« toto », 14) » ?
def dit_bonjour(nom, age):
phrase = f"Bonjour {nom}, vous avez {age} ans."
return phrase Attention : remarquez bien les guillemets autour du paramètre « toto » (c’est une chaîne de caractères)
Les paramètres ne sont pas obligatoires.
À faire vous-même 32
Tester la fonction suivante :
def ma_fon():
return "voici une fonction qui ne sert à rien"
Il faut aussi savoir qu’une fonction ne renvoie pas forcément de valeur (le mot clé return n’est pas obligatoire). Mais si elle ne renvoie pas de valeur, que fait-elle ? Elle peut faire plein de choses, par exemple elle peut tout simplement afficher une chaîne de caractères à l’aide d’un « print« . Sachez que dans certains langages, on utilise les termes méthode ou procédure pour qualifier une fonction « qui ne renvoie rien ».
À faire vous-même 33
Soit le programme suivant :
def dit_bonjour(nom, age):
phrase = f"Bonjour {nom}, vous avez {age} ans."
print(phrase) Tester la fonction dit_bonjour à l’aide de la console (avec par exemple un dit_bonjour(« toto », 14))
À faire vous-même 34
L’indice de masse corporelle (IMC) est une grandeur qui permet d’estimer la corpulence d’une personne.
Il se calcule en fonction de la taille en mètre et de la masse en kilogramme.
La formule est IMC= masse / taille²
Écrire une fonction imc(masse,taille) qui retourne l’indice de la masse corporelle.