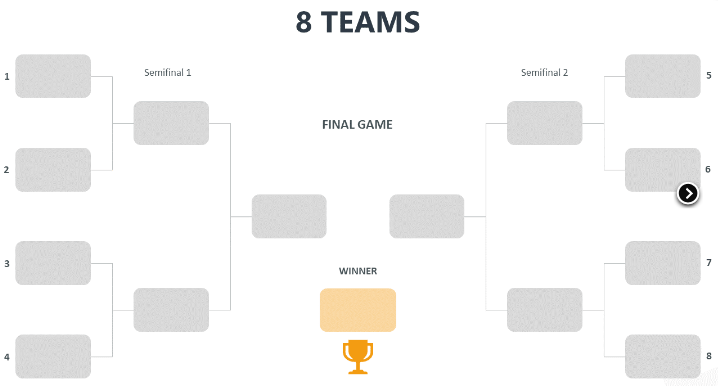
Beaucoup de tournoi sportif sont organisés avec une structure qui représente les matchs joués ou à jouer dans le tournoi. Le principe de base est que chaque branche rassemble deux joueurs (ou deux équipes). Le gagnant avance et le perdant est éliminé. C’est en tout cas le fonctionnement avec élimination Directe.
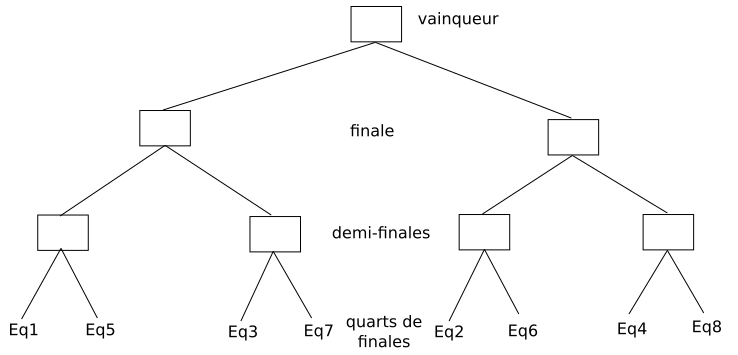
Ce graphique si on commence par le vainqueur ressemble à un arbre.
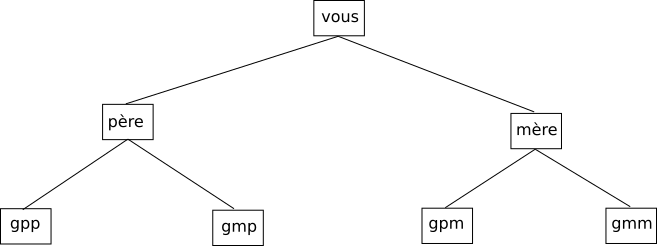
Nous avons ci-dessous ce que l’on appelle une structure en arbre. On peut aussi retrouver cette même structure dans un arbre généalogique :
Dernier exemple, les systèmes de fichiers dans les systèmes de type UNIX ont aussi une structure en arbre.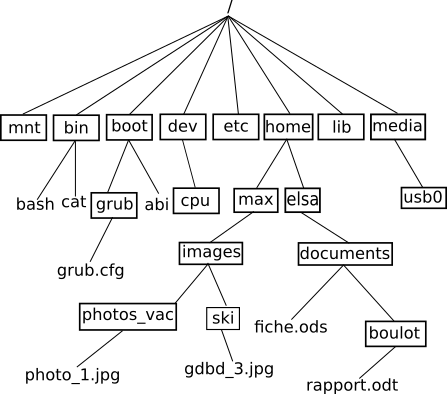 système de fichiers de type UNIX
système de fichiers de type UNIX
Les arbres sont des types abstraits très utilisés en informatique. On les utilise notamment quand on a besoin d’une structure hiérarchique des données : dans l’exemple ci-dessous le fichier grub.cfg ne se trouve pas au même niveau que le fichier rapport.odt (le fichier grub.cfg se trouve « plus proche » de la racine / que le fichier rapport.odt). On ne pourrait pas avec une simple liste qui contiendrait les noms des fichiers et des répertoires, rendre compte de cette hiérarchie (plus ou moins « proche » de la racine). On trouve souvent dans cette hiérarchie une notion de temps (les quarts de finale sont avant les demi-finales ou encore votre grand-mère paternelle est née avant votre père), mais ce n’est pas une obligation (voir l’arborescence du système de fichiers).
Les arbres binaires sont des cas particuliers d’arbre : l’arbre du tournoi de rugby et l’arbre « père, mère… » sont des arbres binaires, en revanche, l’arbre représentant la structure du système de fichier n’est pas un arbre binaire. Dans un arbre binaire, on a au maximum 2 branches qui partent d’un élément (pour le système de fichiers, on a 7 branches qui partent de la racine : ce n’est donc pas un arbre binaire). Dans la suite nous allons uniquement travailler sur les arbres binaires.
Soit l’arbre binaire suivant :
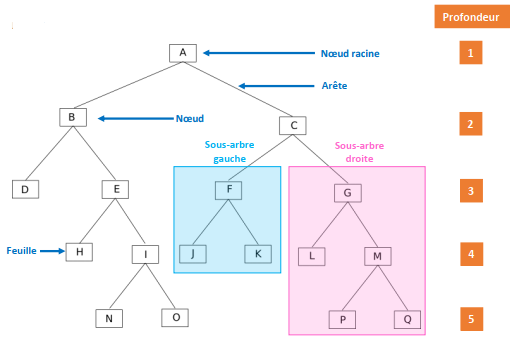
Un peu de vocabulaire :
- chaque élément de l’arbre est appelé noeud (par exemple : A, B, C, D,…,P et Q sont des noeuds)
- le noeud initial (A) est appelé noeud racine ou plus simplement racine
- On dira que le noeud E et le noeud D sont les fils du noeud B. On dira que le noeud B est le père des noeuds E et D
- Dans un arbre binaire, un noeud possède au plus 2 fils
- Un noeud n’ayant aucun fils est appelé feuille (exemples : D, H, N, O, J, K, L, P et Q sont des feuilles)
- À partir d’un noeud (qui n’est pas une feuille), on peut définir un sous-arbre gauche et un sous-arbre droite (exemple : à partir de C on va trouver un sous-arbre gauche composé des noeuds F, J et K et un sous-arbre droit composé des noeuds G, L, M, P et Q)
- On appelle arête le segment qui relie 2 noeuds.
- On appelle profondeur d’un nœud ou d’une feuille dans un arbre binaire le nombre de nœuds du chemin qui va de la racine à ce nœud. La racine d’un arbre est à une profondeur 1, et la profondeur d’un nœud est égale à la profondeur de son prédécesseur plus 1. Si un noeud est à une profondeur p, tous ses successeurs sont à une profondeur p+1. Exemples : profondeur de B = 2 ; profondeur de I = 4 ; profondeur de P = 5
ATTENTION : on trouve aussi dans certains livres la profondeur de la racine égale à 0 (on trouve alors : profondeur de B = 1 ; profondeur de I = 3 ; profondeur de P = 4). Les 2 définitions sont valables, il faut juste préciser si vous considérez que la profondeur de la racine est de 1 ou de 0. - On appelle hauteur d’un arbre la profondeur maximale des nœuds de l’arbre. Exemple : la profondeur de P = 5, c’est un des noeuds les plus profond, donc la hauteur de l’arbre est de 5.
ATTENTION : comme on trouve 2 définitions pour la profondeur, on peut trouver 2 résultats différents pour la hauteur : si on considère la profondeur de la racine égale à 1, on aura bien une hauteur de 5, mais si l’on considère que la profondeur de la racine est de 0, on aura alors une hauteur de 4.
Il est aussi important de bien noter que l’on peut aussi voir les arbres comme des structures récursives : les fils d’un noeud sont des arbres (sous-arbre gauche et un sous-arbre droite dans le cas d’un arbre binaire), ces arbres sont eux mêmes constitués d’arbres…
À faire vous-même 1
Trouvez un autre exemple de données qui peuvent être représentées par un arbre binaire (dans le domaine de votre choix). Dessinez au moins une partie de cet arbre binaire. Déterminez la hauteur de l’arbre que vous aurez dessiné.
Python ne propose pas de façon native l’implémentation des arbres binaires. Mais nous aurons, plus tard dans l’année, l’occasion d’implémenter des arbres binaires en Python en utilisant un peu de programmation orientée objet.
Nous aurons aussi très prochainement l’occasion d’étudier des algorithmes permettant de travailler sur les arbres binaires.
Définition des parcours sur les arbres
FICHE REVISION

Merci à l’auteur : David Roche