Diviser pour régner
Le diviser pour régner est une méthode algorithmique basée sur le principe suivant :
On prend un problème (généralement complexe à résoudre), on divise ce problème en une multitude de petits problèmes, l’idée étant que les « petits problèmes » seront plus simples à résoudre que le problème original. Une fois les petits problèmes résolus, on recombine les « petits problèmes résolus » afin d’obtenir la solution du problème de départ.
Le paradigme « diviser pour régner » repose donc sur 3 étapes :
- DIVISER : le problème d’origine est divisé en un certain nombre de sous-problèmes
- RÉGNER : on résout les sous-problèmes (les sous-problèmes sont plus faciles à résoudre que le problème d’origine)
- COMBINER : les solutions des sous-problèmes sont combinées afin d’obtenir la solution du problème d’origine.
Les algorithmes basés sur le paradigme « diviser pour régner » sont très souvent des algorithmes récursifs.
Nous allons maintenant étudier un de ces algorithmes basés sur le principe diviser pour régner : le tri-fusion
Tri-fusion
Nous avons déjà étudié des algorithmes de tri : le tri par insertion et le tri par sélection. Nous allons maintenant étudier une nouvelle méthode de tri, le tri-fusion. Comme pour les algorithmes déjà étudiés, cet algorithme de tri fusion prend en entrée un tableau non trié et donne en sortie, le même tableau, mais trié.
À faire vous-même 1
Étudiez cet algorithme :
TRI FUSION (tableau):
• Si tableau est de taille <= 1 on ne fait rien.
• Sinon, On sépare tableau en 2 parties gauche et droite,
• On appelle Tri fusion sur gauche et sur droite
• On fusionne gauche et droite dans tableau
FUSIONNER (`tableau`, `gauche`, `droite`):
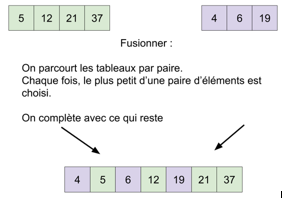
* On parcourt les deux tableaux `gauche` et `droite` en même temps,
Pour chaque paire d'éléments, on place le plus petit dans tableau.
* S'il reste des éléments dans `gauche` ou dans `droite` on les place à la fin
de tableau Pour trier un tableau A, on fait l’appel initial TRI-FUSION(A, 1, A.longueur)
Rappel : Attention, en algorithmique, les indices des tableaux commencent à 1
Cet algorithme est un peu difficile à appréhender, on notera qu’il est composé de deux fonctions FUSIONNER et TRI-FUSION (fonction récursive). La fonction TRI-FUSION assure la phase « DIVISER » et la fonction FUSION assure les phases « RÉGNER » et « COMBINER ».
Voici un exemple d’application de cet algorithme sur le tableau A = [23, 12, 4, 56, 35, 32, 42, 57, 3] :
À faire vous-même 2
Étudiez attentivement le schéma ci-dessous afin de mieux comprendre le principe du tri-fusion (identifiez bien les phases « DIVISER » et « COMBINER »).
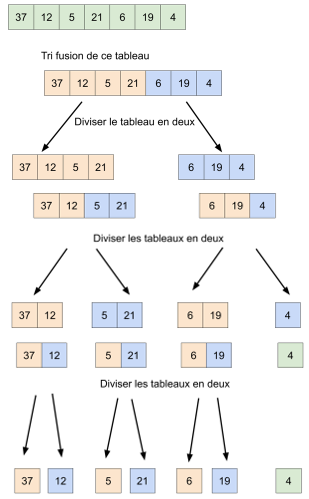
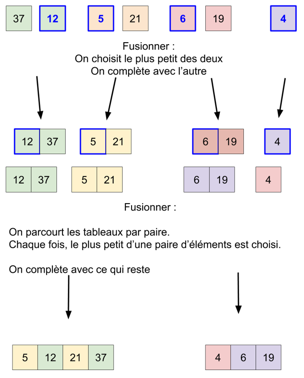
On remarque que dans le cas du tri-fusion, la phase « RÉGNER » se réduit à sa plus simple expression, en effet, à la fin de la phase « DIVISER », nous avons à trier des tableaux qui comportent un seul élément, ce qui est évidemment trivial.
À faire vous-même 3
Reprenez tout le raisonnement qui vient d’être fait sur le tableau T = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]. Vous n’hésiterez pas à faire un schéma et à expliquer la fusion de 2 tableaux triés.
Nous avons vu que le tri par insertion et tri par sélection ont tous les deux une complexité O(n2)
. Qu’en est-il pour le tri-fusion ?
Le calcul rigoureux de la complexité de cet algorithme sort du cadre de ce cours. Mais, en remarquant que la première phase (DIVISER) consiste à « couper » les tableaux en deux plusieurs fois de suite, intuitivement, on peut dire qu’un logarithme base 2 doit intervenir. La deuxième phase consiste à faire des comparaisons entre les premiers éléments de chaque tableau à fusionner, on peut donc supposer que pour un tableau de n éléments, on aura n comparaisons. En combinant ces 2 constations on peut donc dire que la complexité du tri-fusion est en O(n.log(n))
(encore une fois la « démonstration » proposée ici n’a rien de rigoureux).
La comparaison des courbes de la fonction n2 (en rouge) et n.log(n)
(en bleu) :
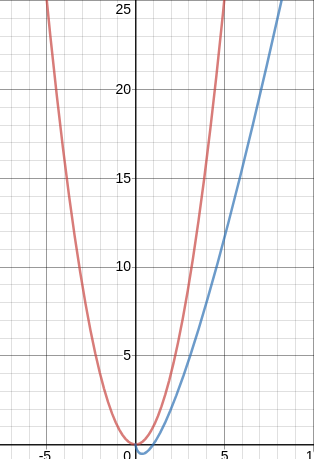
nous montre que l’algorithme de tri-fusion est plus « efficace » que l’algorithme de tri par insertion ou que l’algorithme de tri par sélection.
Présentation vidéo détaillée du tri fusion
Utilisation du tri fusion:
Contrairement au tri par sélection ou par insertion, le tri fusion est réellement utilisé en pratique.
Il a de nombreux avantages :
• complexité optimale (cela ne signifie pas qu’il est le plus rapide)
• stable (voir plus bas)
• facile à mettre en œuvre
Cependant, il est possible d’améliorer la méthode :
timsort, le tri natif en Python et Javascript utilise une combinaison du tri fusion et du tri par insertion.

Auteur : David Roche