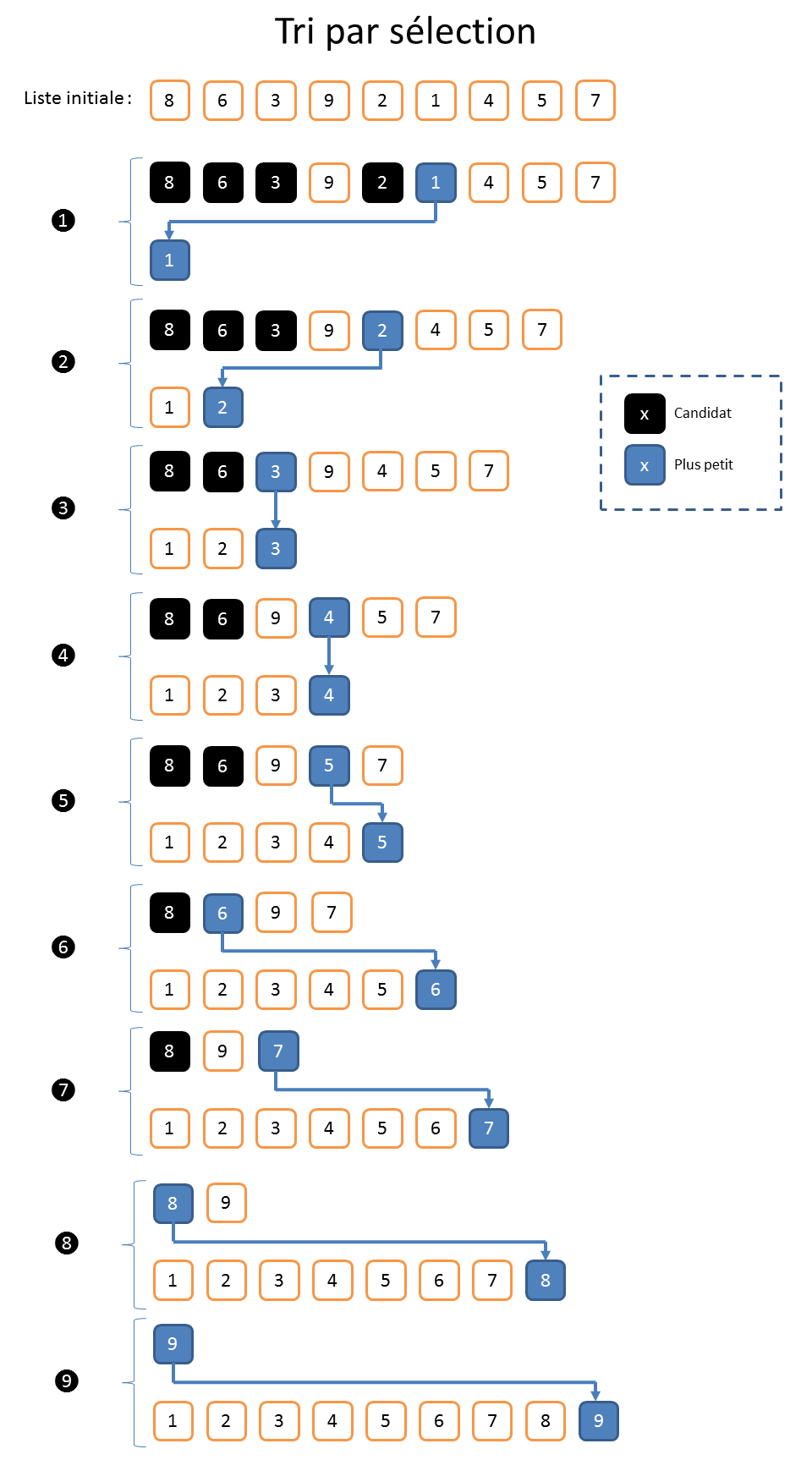
Pour simplifier nous allons trier une liste de 9 valeurs

[ 8, 6, 3, 9, 2, 1, 4, 5, 7 ]

pour commencer l’explication , utilisons 2 listes

A faire: sur le document réponse Libre Office.

Réaliser le même schéma avec [ 5, 12, 3, 7, 4 ] sur le document réponse Libre Office. En fin de document vous pouvez découper les numéros pour faire une simulation à la main.

Combien de comparaison? pour trier [ 8, 6, 3, 9, 2, 1, 4, 5, 7 ]

pour sélectionner l’élément le plus petit on liste les 9 valeurs et on fait 8 comparaisons, pour le deuxième on fait 7 comparaisons, pour le troisième 6 comparaisons et ainsi de suite. D’où nombre de comparaison= 8+7+6+….+1=36.

Par extension si notre liste est constituée de n valeurs, le nombre de comparaison = (n-1)+(n-2)+(n-3)+ …..+3+2+1 en factorisant nombre de comparaison=n*(n-1) /2 soit n²/2-n/2 .

On dit que l’algorithme de tri par sélection a donc une complexité en O(n²). On parle aussi de complexité quadratique.

Voici une implémentation sous python avec 2 tableaux ou listes comme le graphique ci dessus

def tri_selection(tableau):
    '''tri d'un tableau, l'argument tableau est un tableau ou liste, la fonction renvoie un autre tableau ou liste resultat'''
    resultat = [] 
    longueur = len(tableau)                 
    
    while len(resultat) != longueur:        
        minimum = tableau[0]                   
        
        for i in range(1, len(tableau)):        
            if minimum > tableau[i]:                
                minimum = tableau[i]                    
        resultat.append(minimum)                
        tableau.remove(minimum)                 
    return resultat 

voici l’algorithme du tri par sélection ( ici une seule liste )

• PROCEDURE tri_Selection ( Tableau a[1:n])
•     POUR i VARIANT DE 1 A (n – 1) FAIRE
•         TROUVER [j] LE PLUS PETIT ELEMENT DE [i + 1:n];
•         ECHANGER [j] ET [i];
• FIN PROCEDURE;

en python à essayer

def tri_selection(tab):
   print(tab)
   for i in range(len(tab)):#boucle sur toute la liste
      # Trouver le min
       min = i
       for j in range(i+1, len(tab)):
           if tab[min] > tab[j]:
               min = j

       tmp = tab[i]
       print('tmp',tmp)#affiche tmp pour visualiser l'algo
       tab[i] = tab[min]
       print ('tab1',tab)#affiche la liste tab pour visualiser l'algo
       tab[min] = tmp
       print('tab2',tab)#affiche la liste tab pour visualiser l'algo
   return tab
# Programme principale pour tester le code ci-dessus
tab = [98, 22, 15, 32, 2, 74, 63, 70]#changer les valeurs de la liste pour un autre essai

tri_selection(tab)

print ("Le tableau trié est:")
print (tab)

vous pouvez trouver des explications supplémentaire ici:

site de podcastscience , site de David Roche et sur le site http://lwh.free.fr

Retour vers article algorithme de tri