|
This page was exported from Enseignement de l'informatique et du numérique au lycée Boissy d'Anglas
[ https://icn-isn-boissy.yj.fr/wp ] Export date: Sun Feb 8 7:50:42 2026 / +0000 GMT |
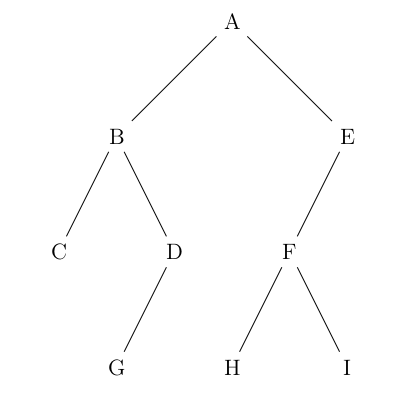
Exercices -ArbresExercice 12021, sujet 0 Question 1 Déterminer la taille et la hauteur de l'arbre binaire suivant : Question 2 On décide de numéroter en binaire les nœuds d'un arbre binaire de la façon suivante :
Par exemple, dans l'arbre ci-dessous, on a utilisé ce procédé pour numéroter les nœuds A, B, C, E et F . 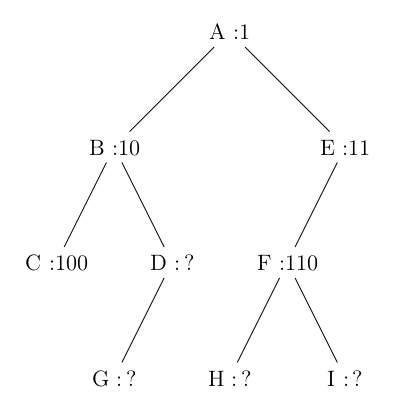
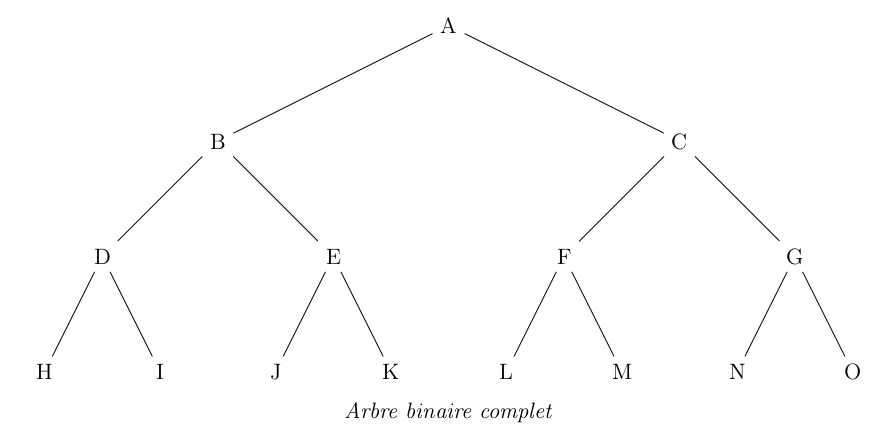
Question 3 On décide de représenter un arbre binaire complet par un tableau de taille n + 1, où n est la taille de l'arbre, de la façon suivante :
Répondre aux questions suivantes :
Question 4 On se place dans le cas particulier d'un arbre binaire de recherche complet où les nœuds contiennent des entiers et pour lequel la valeur de chaque noeud est supérieure à celles des noeuds de son fils gauche, et inférieure à celles des noeuds de son fils droit. Écrire une fonction merci à G.Lassus Exercice 22021, Métropole sujet 1, exercice 1 Dans cet exercice, les arbres binaires de recherche ne peuvent pas comporter plusieurs fois la même clé. De plus, un arbre binaire de recherche limité à un nœud a une hauteur de 1. On considère l'arbre binaire de recherche représenté ci-dessous (figure 1), où 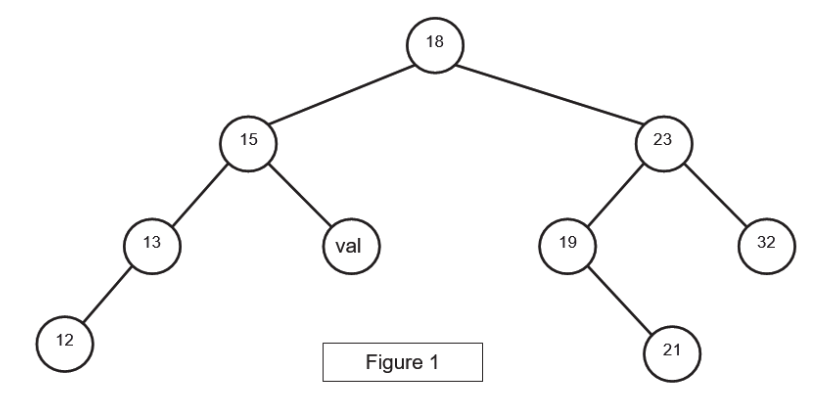 1.a Donner le nombre de feuilles de cet arbre et préciser leur valeur (étiquette). 1.b Donner le sous arbre-gauche du nœud 23. 1.c Donner la hauteur et la taille de l'arbre. 1.d Donner les valeurs entières possibles de On suppose, pour la suite de cet exercice, que 2. On rappelle qu'un parcours infixe depuis un nœud consiste, dans l'ordre, à faire un parcours infixe sur le sous arbre-gauche, afficher le nœud puis faire un parcours infixe sur le sous-arbre droit. a. Donner les valeurs d'affichage des nœuds dans le cas du parcours infixe de l'arbre. 3. On considère la classe 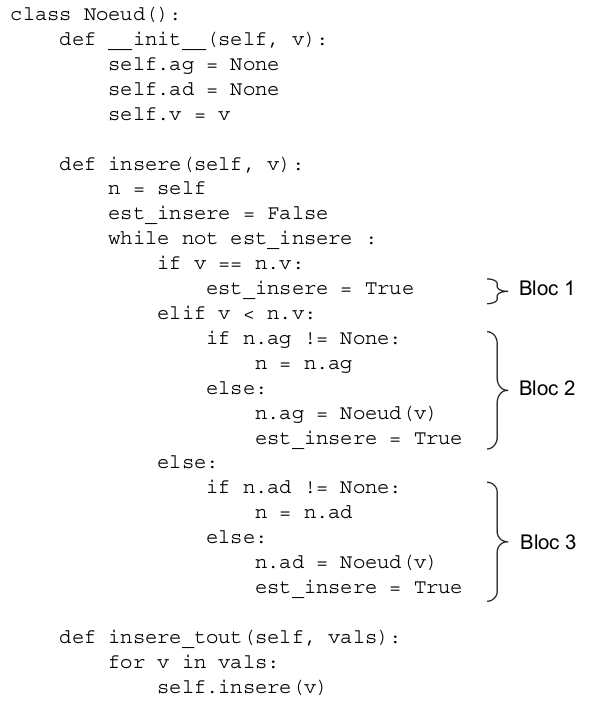 a. Représenter l'arbre construit suite à l'exécution de l'instruction suivante : b. Écrire les deux instructions permettant de construire l'arbre de la figure 1. On rappelle que le nombre c. On considère l'arbre tel qu'il est présenté sur la figure 1. Déterminer l'ordre d'exécution des blocs (repérés de 1 à 3) suite à l'application de la méthode 4. Écrire une méthode Exercice 32021, Métropole Candidats Libres 2, exercice 3 On rappelle qu'un arbre binaire est composé de nœuds, chacun des nœuds possédant éventuellement un sous-arbre gauche et éventuellement un sous-arbre droit. Un nœud sans sous-arbre est appelé feuille. La taille d'un arbre est le nombre de nœuds qu'il contient ; sa hauteur est le nombre de nœuds du plus long chemin qui joint le nœud racine à l'une des feuilles. Ainsi la hauteur d'un arbre réduit à un nœud, c'est-à-dire la racine, est 1. Dans un arbre binaire de recherche, chaque nœud contient une clé, ici un nombre entier, qui est :
Un arbre binaire de recherche est dit « bien construit » s'il n'existe pas d'arbre de hauteur inférieure qui pourrait contenir tous ses nœuds. On considère l'arbre binaire de recherche ci-dessous. 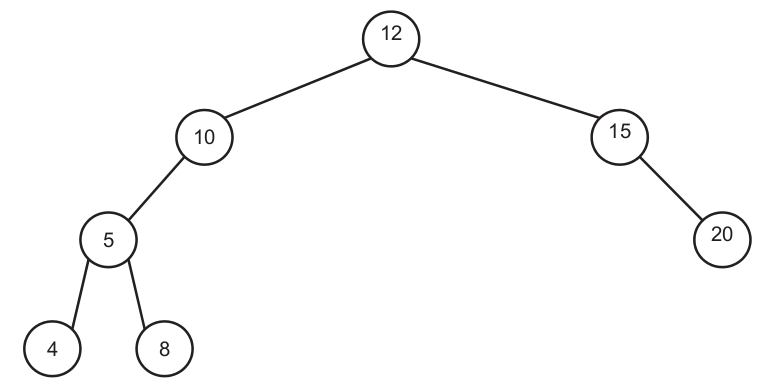 1.a. Quelle est la taille de l'arbre ci-dessus ? 1.b. Quelle est la hauteur de l'arbre ci-dessus ? 2. Cet arbre binaire de recherche n'est pas « bien construit ». Proposer un arbre binaire de recherche contenant les mêmes clés et dont la hauteur est plus petite que celle de l'arbre initial. 3. Les classes Noeud et Arbre ci-dessous permettent de mettre en œuvre en Python la structure d'arbre binaire de recherche. La méthode Donner la représentation de l'arbre codé par les instructions ci-dessous. 4. Pour calculer la hauteur d'un arbre non vide, on a écrit la méthode ci-dessous dans la classe Noeud. Écrire la méthode 5. Écrire les méthodes 6. On souhaite écrire une méthode On rappelle que la taille maximale d'un arbre binaire de recherche de hauteur est 2h-1. . 6.a Quelle est la taille minimale, notée 6.b Écrire la méthode |
|
Post date: 2022-10-14 08:30:02 Post date GMT: 2022-10-14 06:30:02 Post modified date: 2022-11-17 08:19:42 Post modified date GMT: 2022-11-17 07:19:42 |
| Powered by [ Universal Post Manager ] plugin. HTML saving format developed by gVectors Team www.gVectors.com |