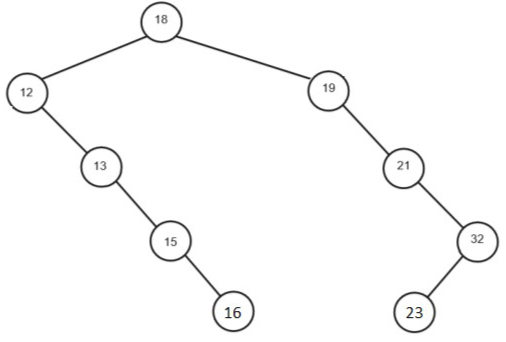
1.a. Il y a 4 feuilles, d’étiquette 12, val, 21 et 32.
1.b. Le sous-arbre gauche du nœud 23 est 19-21.
1.c. La hauteur de l’arbre est 4. Sa taille est 9.
1.d. Les valeurs possibles de val sont 16 et 17.

2.a. Parcours infixe : 12-13-15-16-18-19-21-23-32
2.b. Parcours suffixe : 12-13-16-15-21-19-32-23-18

3.a.

3.b.

racine = Noeud(18)
racine.insere([15, 13, 12, 16, 23, 32, 19, 21])

(d’autres solutions sont possibles)

3.c. bloc 3 – bloc 2
ne rentre pas dans bloc 1

4.

class Noeud():
    def __init__(self, v):
        self.ag = None
        self.ad = None
        self.v = v

    def insere(self, v):
        n = self
        est_insere = False
        while not est_insere:
            if v == n.v:
                est_insere = True
            elif v < n.v:
                if n.ag != None:
                    n = n.ag
                else:
                    n.ag = Noeud(v)
                    est_insere = True
            else:
                if n.ad != None:
                    n = n.ad
                else:
                    n.ad = Noeud(v)
                    est_insere = True

    def insere_tout(self, vals):
        for v in vals:
            self.insere(v)

    def recherche(self, v):
        arbre = self
        while not arbre is None:
            if arbre.v == v:
                return True
            if v < arbre.v:
                arbre = arbre.ag
            else:
                arbre = arbre.ad
        return False


    # version récursive (non demandée)

    def recherche_rec(self, v):
        if self is None:
            return False
        if self.v == v:
            return True
        if v < self.v:
            if self.ag is not None:
                return self.ag.recherche_rec(v)
            else:
                return False
        else:
            if self.ad is not None:
                return self.ad.recherche_rec(v)
            else:
                return False


racine = Noeud(18)
racine.insere_tout([12, 13, 15, 14, 19, 21, 32, 23])
print(racine.recherche(149))
print(racine.recherche(12))