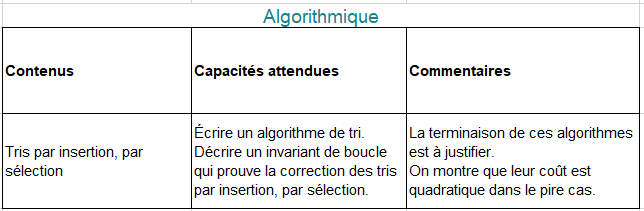
Référence au programme de NSI

On veut trier une liste lorsqu’on pense que ses éléments sont dans le désordre, ou plus précisément dans un ordre qui ne nous convient pas. L’objectif du tri, en tant qu’algorithme, est de mettre les éléments dans le bon ordre. Par exemple sur STRAVA qui est un site et une application mobile pour enregistrer les activités sportives, l’utilisateur peut classer ses activités par années, semaines, distances parcourues, temps sur certains parcours mythiques (segment) .

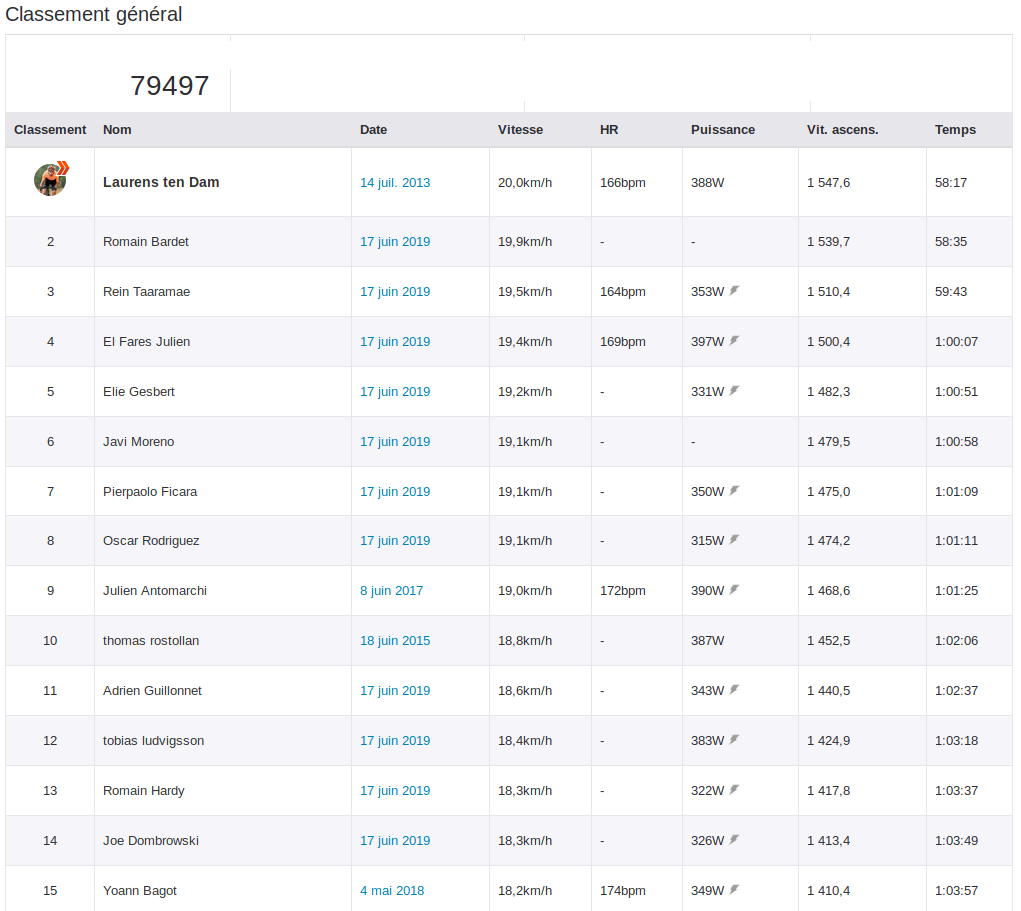
Sur ce tableau le classement est réalisé sur le temps d’ascension, par ordre croissant.

Nous allons étudier 2 algorithmes de tri :

(cliquez pour ouvrir les articles)

le tri par sélection et le tri par insertion.

Nous avons calculer le nombre comparaison que faisait les algorithmes dans le tri par insertion et sélection, On parle de complexité . La complexité d’un tri de « n » éléments se note avec un « omicron » : dites « grand O ». Par exemple, la complexité du « tri par sélection » sera en « O(n*(n-1) /2 ) », où « n*(n-1) /2 » est la formule qu’on avait utilisée un peu plus tôt. Comme on s’intéresse à des valeurs importantes et qu’on ne veut qu’un « ordre de grandeur », on considérera que cette « complexité » peut se « simplifier » en « O(n*(n-1)) », qui peut elle-même se simplifier en « O(n²) ». On dira que l’algorithme du « tri par sélection » est de « complexité quadratique » en « O(n²) ».

Pour notre classement il y a 80 000 valeurs à trier voici un tableau résumant le nombre d’opération et une estimation du temps en supposant qu’une opération dure 1 ms.

Nombre d’éléments « n »	Nombre d’opérations pour un tri en « O(n²) »	Durée pour un tri en « O(n²) »
10	100	100 ns
100	10 000	10 us
1 000	1 000 000	1 ms
10 000	100 000 000	100 ms
100 000	10 000 000 000	10 s
1 000 000	1 000 000 000 000	16 min 40 s
10 000 000	100 000 000 000 000	27 heures
100 000 000	10 000 000 000 000 000	115 jours
1 000 000 000	1 000 000 000 000 000 000	31 ans

Il y a 1.2 millions d’utilisateur de Strava , 3.4 milliard d’utilisateur de Facebook . Les données à trier ne manquent pas….Et le temps de les trier elles seront peut être obsolètes.

Comment faire ? Il existe des algorithmes de tri plus performant: Tri à bulles , Tri rapide , ….

A faire:

Essai évaluation par le temps d’exécution du programme de tri:

Estimation de complexité par le temps d’exécution (approximation car le temps d’exécution d’un algorithme est aussi lié à d’autres paramètres… )

En ouvrant et exécutant le programme de tri :

tris-avec_evaluation-temps-execution_programme.py

à télécharger en fin d’article.

 extrait du programme

# tri rapide avec affichage du temps passé
 debut_chrono=time.time() # lancement chrono
 trirapide(L) # lancement du tri
 temps_exe=time.time()-debut_chrono #arret chrono et calcul du temps 
 print("nombre de valeur =",len(L)) # affichage nb valeurs
 print("temps execution tri rapide =",temps_exe) # affichage crhono

Essayer de lancer ce programme en testant une liste aléatoire de 10, 100 , 1000, 10000 valeurs, faire un classement des tris.

Maintenant au lieu de trier une liste aléatoire, trions une liste déjà triée. Refaites votre classement .

Quelles conclusions tirez vous de vouloir classer la complexité d’un algorithme par son temps d’exécution?

(Rappel les deux algorithme fusion et insertion ont la même complexité)

Mini projet:

Amélioration , Il vaudrait mieux compter le nombre d’opération de comparaison dans l’algorithme de tri. Proposer une solution de compteur dans le programme de tri de votre choix

vous trouverez ici tous les fichiers à télécharger.